Ведийские алтари и геометрия древней Индии
Древнекитайский "Трактат о гномоне"
Математическая загадка "Книги Перемен"
Ведийские алтари и геометрия древней Индии
Формы и размеры ведийских алтарей для жертвоприношений были предписаны шастрами. При этом указывалось, что отклонения от указанных форм или размеров аннулируют эффект ритуала.
Три основных алтаря, Три огня, на которых должны были совершаться обязательные жертвоприношения, упоминались в Ригведе; Правила их построения там не давались, но говорилось, что для этого есть специалисты. Размеры и формы алтарей приводились в Шатапатха брахмане (усл. –2000 - –600 гг.), Тайттирия самхите. Там же упоминались и геометрические фигуры, связанные с построением алтарей, в частности, пифагорейские треугольники. "Прослеживая историю треугольника (15, 36, 39) <= 3*(5, 12, 13)> мы впервые встречаем его в Майтрайане самхите, Шатапатха брахмане. Упоминались только 15 и 36 но не 39"[1]. Три огня строились из кирпичей; имели форму круга, квадрата, полукруга и одинаковую каноническую площадь в 7.5 кв. purusa. Алтарь Маха веди для жертвоприношений Сомы имел форму равнобедренной трапеции с основаниями a = 30, b = 24 и высотой h = 36 padas. Алтари для жертвоприношений Kamya agni имели форму сокола, колеса, черепахи, ромба,… и каноническую площадь. Дошедшие до нашего времени Шульба сутры (усл. –V - –IV вв.) описывали способы построения алтарей с помощью верёвки[2].
Шульба сутры представляли собой учебники по геометрии. В них определялись простые геометрические объекты; описывались их свойства, способы их построения с помощью верёвки; ставились и разрешались определённые геометрические задачи, в т.ч. 1) преобразования фигур с сохранением площади (построение фигуры данной площади, но другой формы); 2) преобразование фигур с сохранением формы, но другой площади. Среди задач на преобразование фигур с сохранением площади была "квадратура круга" – построение круглого алтаря данной площади, т.е. равновеликого данному квадратному алтарю. Среди утверждений Шульба сутра имелась и "теорема Пифагора"; она формулировалась не для прямоугольного треугольника, а для диагонали прямоугольника. Доказательство её в сутрах не давалось; самое раннее из известных индийских доказательств этой теоремы относится к +V - +VI вв. Теорема Пифагора использовалась в задаче превращения прямоугольника в квадрат той же площади. В Шульба сутрах встречались пифагорейские треугольники: (3, 4, 5), (5, 12, 13) (в т.ч. в размерах алтаря Маха веди, неявно), (7, 24, 25), (8, 15, 17), (12, 35, 37).
Все задачи и теоремы Шульбы сутр имели целью построение алтарей заданных форм и размеров. В частности, задачи на построение фигур, равновеликих данной (квадрата или круга, равновеликого данному прямоугольнику и пр.) были обусловлены требованием сохранения у алтарей канонической площади. Хотя современные датировки Шульба сутр относят их составление ко времени, гораздо более позднему, чем ведическое, однако, поскольку они использовались для построения ведических алтарей канонизированных форм и размеров, то почти несомненно, что основные приведённые в них задачи и методы их решения – в частности и в особенности преобразование прямоугольника в равновеликий квадрат, а также связанная с этой проблемой теорема Пифагора – были известны, в той или иной форме не позднее ведийского времени. Об этом свидетельствуют и ссылки на некоторую авторитетную древнюю традицию у авторов сутр. Пифагорейские же тройки напрямую упоминаются в Шатапатха брахмане, а для алтаря Маха веди размеры, как нетрудно видеть, были специально подобраны так, чтобы в нем "содержались" первые два пифагорейских треугольника (3, 4 ,5) и (5, 12, 13); см. выше.
Итак, ведические арьи (точнее, брахманы), прибывшие в Индию, по современным оценкам около –XV в., имели следующие математические знания: 1) первых пифагорейских троек (несомненно); 2) постановки и решения задач на преобразование прямоугольника в равновеликий квадрат; 3) теоремы Пифагора (почти несомненно). Точно такие же математические знания имелись примерно на триста лет раньше (по современным датировкам) в вавилонской математике.
Кроме того, некоторые геометрические фигуры и числовые константы (в т.ч. первые пифагорейские тройки) в ведийской культуре были канонизированы и связаны с ритуальными объектами – использованы при построении алтарей. Сходная связь математики и религии имелась в пифагореизме; восходила от него к вавилонской культуре, и далее, видимо, к более раннему общему первоисточнику.
Древнекитайский "Трактат о гномоне".
"Трактат о гномоне" (Чжоу би)[3] – самый древний китайский математический и астрономический текст. Его составление относят ко времени между –1000 и –100 гг. Астрономическую часть трактата датируют, по косвенным соображениям, –VII - –VI вв.
Первым известным комментатором трактата был математик +III века Чжао Цзюньцин. Следующие комментаторы – Чжэнь Луань, современник династии Северная Чжоу (557- 81 гг.), Ли Чуньфэн, современник династии Тан (618 - 907 гг.). В эпоху Тан, когда математика была выделена как самостоятельный предмет, Чжоу би вошел в "Десятикнижие" ("Десять книг счетного канона"), сборник основных математических текстов.
"Трактат о гномоне" состоит из двух свитков (цзюаней). В первом записана беседа Чжоу гуна (–XI в.), брата первого императора династии Чжоу, с сановником Шан Гао, "весьма искусным в математике", как сказано в тексте трактата. Во втором свитке – беседа Чэнь цзы с его учеником Жун Фаном. Первый свиток посвящен математическим вопросам. В нём упоминается пифагорейская тройка (3, 4, 5); приводится теорема Пифагора в применении к этой тройке; рассматривается использование угольника (прямоугольного треугольника) для решения практических задач, в частности определения, методом подобия, высот удалённых объектов. Во втором свитке рассматриваются астрономические вопросы, иньский календарь, космологическая теория гай-тянь ("небо-покрывало").
Название трактата, "Чжоу би" (би – шест для измерения тени; гномон) объясняется так. Жун Фан спрашивает: "Что такое "Чжоу би"?" Чэнь цзы отвечает: "В древности правители построили [город] Чжоу, это число [8 чи, длина шеста - би] происходит из династии Чжоу, поэтому этот шест называется Чжоу би". Чжоу – столица династии Чжоу, позже г. Лоян. Чи – единица измерения, примерно 1/3 метра.
Теорема Пифагора, частный случай которой упоминался в "Трактате о гномоне", доказывалась в комментарии Чжао Цзюньцина. Она называлась там "метод гоу-гу"; гоу - меньший, гу - больший катет прямоугольного треугольника. Чжао приводил (словесно описанные) геометрические методы решения квадратных уравнений и сводящихся к ним задач, связанных с прямоугольными треугольниками, соответствующие греческой геометрической алгебре. Задачи на подобие, использующие прямоугольный треугольник, также рассматривались Чжао и другими китайскими математиками.
Первую, математическую часть трактата начинает вопрос Чжоу гуна, обращённый к Шан Гао: как можно производить расчёты размеров земных и небесных объектов, "ведь не существует лестницы, поднимающейся к Небу и нельзя измерить размеры Земли с помощью чи и цуней[4]. Скажите, как же тогда были получены нужные числа?"[5]
Шан Гао отвечает: "Методы вычислений происходят из круга и квадрата. Круг происходит из квадрата, квадрат происходит из угольника, угольник происходит [из таблицы умножения] "девятью девять - восемьдесят один"".
Выражение "круг происходит из квадрата, квадрат происходит из угольника", вероятно, отсылает к методами построения соответствующих фигур, сводимым, в конечном счёте, к использованию угольника (прямоугольного треугольника). Квадрат очевидным образом строится с помощью угольника, а построение с помощью угольника круга (вращением вокруг вершины) описано далее в "Трактате".
Чжао Цзюньцинь комментировал это место "Трактата" так:
"Если диаметр круга равен 1, то длина его окружности равна 3. Если сторона квадрата равна 1, то его периметр равен 4. Можно разрезать круг, выпрямив его как [меньший катет] гоу прямоугольного треугольника, расправить квадрат как [больший катет] гу прямоугольного треугольника. Если соединить концы, то гипотенуза будет равна 5. Это и есть связь между кругом и квадратом. Поэтому говорят: "Числовые методы происходят из круга и квадрата"".
Таким образом Чжао проиллюстрировал несколько неясную фразу "Трактата" о том, что "числовые методы происходят из круга и квадрата" примером первого пифагорейского треугольника (3, 4, 5). Соотнеся два катета этого треугольника с окружностью радиуса 1 и периметром квадрата со стороной 1, он отметил, что гипотенуза этого угольника – как бы "связывающая" такие круг и квадрат – будет равна 5. Впрочем, комментарий вряд ли сильно прояснил исходную мысль.
Продолжение комментария Чжао:
"Круг и квадрат - это образы Неба и Земли, а также символы Инь и Ян. Чжоу гун спрашивает Шан Гао о теории чисел Неба и Земли. Шан Гао в ответ говорит о круге и квадрате, чтобы указать их (Неба и Земли) формы, нечётными и чётными числами объясняет их вычисления".
Чжоу гун спрашивал Шан Гао о вычислениях размеров земных и небесных объектов – тот начал ответ с рассказа о круге, квадрате, угольнике. Чжао в комментарии указал, что Небо соотносится с кругом, а Землю с квадратом, для построения и вычисления размеров которых имеются методы. При этом он представил один катет угольника длиной окружности (3), а другой – периметром квадрата (4), что аналогично популярному в пифагореизме соотнесению этих катетов с: мужским/ небесным (3) и женским/ земным (4) началами; порождающим, в результате соединения в треугольник, третий элемент, гармонизирующий их, гипотенузу (5).
Продолжение ответа Шан Гао:
"Числа, касающиеся круга, можно получить из квадрата. Квадрат происходит из угольника[6]. Угольник имеет ширину и длину, нужно знать методы умножения и деления. [Треугольная таблица умножения] "девятью девять - восемьдесят один" – источник знания умножения и деления. [Если] начертить угольник, взяв [меньший катет] гу равным 3, [больший катет] гоу равным 4 [то] гипотенуза будет 5. Строим снаружи квадраты [на сторонах треугольника]. Соединим концы, получим 3, 4, 5. Величина угольников 25, это и есть площадь [двух] угольников. С помощью этих методов Юй управлял Поднебесной[7].
Утверждение Шан Гао о том, что угольник (прямоугольный треугольник) с катетами 3 и 4 имеет гипотенузу, равную 5, Чжао воспринял как частный случай применения теоремы Пифагора, и дал, в комментарии к этому утверждению, её общую формулировку:
"Метод гоу и гу: два числа рождают третье, имея [катеты] гоу и гу, вычисляется гипотенуза".
Далее комментатор (Чжао) привёл доказательство теоремы Пифагора, с помощью использования (словесно описанного) "архитектурного чертежа". Такое доказательство встречалось у индийского математика Бхаскары (VI в.). У Эвклида было приведено более сложное доказательство. Далее Чжао привёл геометрические методы решения квадратных уравнений, основанные на применении теоремы Пифагора. Аналогичные методы имелись в древнегреческой математике (у Эвклида), они назывались там приложение площадей, и восходили к вавилонской математике.
Слова Шан гао "с помощью этих методов Юй управлял Поднебесной" Чжао в своём комментарии интерпретировал как использование угольника для определения высот (гор) и глубин (рек), с помощью метода подобия:
"Юй боролся с наводнениями так: смотрел на формы гор и рек и определял глубины и высоты. Покорение гор и обуздание рек было осуществлено благодаря методу гоу-гу".
Такая интерпретация комментатора обоснована нижеследующим ответом Шан Гао на просьбу Чжоу гуна объяснить, как применять угольник для решения практических задач:
"положим одну сторону угольника горизонтально, чтобы [стороной угольника] проверить: является ли линия прямой. Поместим сторону угольника вверх- вертикально – измерим высоту. Поместим сторону угольника вниз- вертикально – измерим глубину. Поместим сторону угольника горизонтально – измерим расстояние между точками".
Вторая и третья фразы ответа Шан Гао, очевидно, представляют собой описание использования угольника, методом подобия, для определения высот или глубин объектов ("гор и рек"), что и отмечено комментатором.
Далее Шан Гао продолжил объяснять использование угольника:
"Зафиксируем точку угольника, вращаем его – получаем круг. Два угольника вместе составляют один квадрат"
Здесь дано описание использования угольника для построения круга и квадрата, о чём говорилось в начале трактата. Чжао комментирует:
"Угольник используют и для измерения вещей, и для построения круга, и для составления квадрата, [поэтому] угольник является универсальным объектом".
Заключительные фразы математической части "Трактата" и комментарии к ним:
Шан Гао: "Квадрат – Земля, Круг – Небо. Небо круглое, Земля квадратная".
Комментарий Чжао Цзюньциня: "Это относится к принципам Инь и Ян, а не к настоящим Небу и Земле. Небо и Землю нельзя увидеть полностью, как же мы можем говорить, что они круглые и квадратные?"
Шан Гао: "Квадрат это основа, из него получается круг…
Тот, кто знает [теорию] Земли умён. Тот, кто знает [теорию] Неба совершенномудрый.
Ум происходит из катета гоу".
Комментарий Чжао Цзюньциня: "Катет гоу есть тень [вещей]. Из рассмотрения катета гоу мы узнаем высоту и длину вещей, поэтому говорится: ум происходит из [катета] гоу".
Фразу Шан Гао "ум происходит из катета гоу" и комментарий к ней Чжао можно понимать так: "используя угольник и методы математики, наш ум познаёт недоступные прямому восприятию вещи", или, в общем смысле: "математика развивает ум".
Шан Гао: [Катет гоу] происходит из угольника. Вычисленное угольником верно для любой вещи".
Чжоу гун: "согласен с Вами".
На этом заканчивается первая (математическая) часть "Трактата о гномоне".
* * *
Астрономический гномон (шест, используемый при измерении высоты Солнца над горизонтом) и его тень образуют угольник. С другой стороны, Чжао, говоря об угольнике, постоянно упоминаемом в "Трактате" в качестве инструмента для решения задач, в том числе по измерению методом подобия высот/ глубин недоступных объектов. назвал его меньший катет тенью: "катет гоу есть тень" – т.е. соотнёс с гномоном.. Таким образом, название трактата "Чжоу би" – чжоусский гномон – может быть переведено и как чжоусский угольник.
* * *
Итак, авторам трактата "Чжоу би" были известны 1) правила счисления (арифметика); 2) простейшие геометрические фигуры, включая прямоугольный треугольник; 3) принципы подобия и их использование на практике; 4) первая пифагорейская тройка; 5) (возможно) теорема Пифагора в применении к ней; 6) использование гномона для определения времени.
При этом 1) упоминаемый в тексте "Трактата" первый пифагорейский треугольник (3, 4, 5) не имел непосредственного применения на практике; 2) персонажи текста приписывали авторство (части) своих знаний полумифическим культурным героям древности; 3) отдельные математические формулировки в трактате имели примитивный, даже утрированный характер и, судя по тексту, плохо понимались самими собеседниками, а судя по комментариям Чжао к этим местам, немногим лучше понимались и через почти тысячу лет; 4) рассмотренные в чжоуском трактате (усл. –X в.) математические идеи и задачи не развивались до эпохи Хань (–III - + III вв.).
Как известно, ранняя китайская цивилизация, начиная с династии Инь (предшествовавшей Чжоу), заимствовала ряд важных инноваций от индоевропейцев (металлургия бронзы, колесницы,…); возможно даже, что основатели династий являлись частично индоевропейцами.
Поскольку все математические знания чжоуского "Трактата" были известны много раньше (древний Вавилон, ведийская Индия,..) то, они также, несомненно, представляли собой заимствования - особенно учитывая их местами утрированный и не имеющий отношения к практике характер. Полутеологические-протофилософские рассуждения в "Трактате", связанные с числами и фигурами, близкие к пифагорейско-халдейской нумерологии, также, скорее всего, представляли собой результаты этого заимствования- трансляции идей, впрочем, со значительными искажениями и примитивизацией, неудивительными, учитывая отдалённость культур во времени и пространстве.
Математическая загадка "Книги Перемен"
В древнем Китае результаты гаданий представлялись сочетаниями шести чисел – шестёрок или девяток – и изображались (в более позднее время) в виде гексаграмм, состоявших из прерывистых или непрерывных (инь или ян) линий. Инь (шестёрка) изображалась прерывистой, ян (девятка) – непрерывной чертой.
В "Книге Перемен" (усл. –XII в.) все возможные 64 результата гадания (64 гексаграммы), были расположены в следующем порядке:
Рис 1. Порядок гексаграмм в "Книге Перемен"
Расположение 64 гексаграмм в "Книге Перемен" (рис. 1) имеет одну хорошо известную закономерность; двадцать восемь последовательных пар гексаграмм с номерами (2n, 2n+1) являются зеркальными отражениями друг друга; за исключением восьми центрально- симметричных, стоящих на местах 0, 1, 26, 27, 28, 29, 60, 61.
По какой закономерности расположены гексаграммы с чётными/ нечётными номерами и есть ли она вообще? Покажем, что такая закономерность имеется.
Расставим номера 64 ГГ "Книги Перемен" в таблице 8*8 следующим образом. Расположим над верхней строкой таблицы 8 триграмм в порядке Вэнь вана (см. ниже рис. 3), а слева от первого столбца – триграммы, являющиеся их зеркальными отражениями. На пересечении столбца и строки поставим номер, на котором находится в "Книги Перемен" гексаграмма, состоящая из двух триграмм – нижней из вертикального столбца, верхней из горизонтальной строки (рис. 2).
Рис. 2.
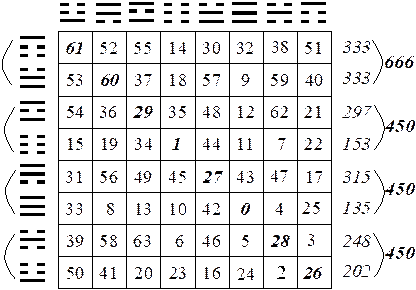
Случайным расположение чисел в таблице быть никак не может:
● В первых двух строках сумма чисел одинакова, и равна 333 (а вместе она составляет весьма значимое число 666).
● Оставшиеся шесть строк разбиваются на пары, сумма чисел в каждой из которых равна 450 (= 30*15).
Итак, расположение чисел в построенной таблице 8*8, представляющей порядок гексаграмм в "Книге Перемен", имеет некоторую закономерность. Следовательно, гексаграммы в "Книге Перемен" тоже расположены по некоторому закону, а не случайно. Этот закон представляет сбой определённую математическую загадку.
Примечание. Как известно, порядок расположения триграмм Вэнь-вана представляет годичный цикл, разбитый на 8 полусезонов[8].
Рис. 3
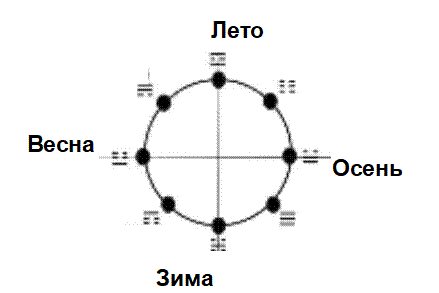
Пары взаимодополнительных (по сумме номеров) рядов из 8 гексаграмм на рис. 2 относятся к парам триграммам, зеркально отражённым по отношению к триграммам, соответствующим одному сезону – т.е. двум полусезонам. Например, третий и четвёртый ряды соответствуют сезону Лето. Это означает, что при расстановке 64 гексаграмм составители "Книги перемен" во-первых, исходили из годового цикла, разбитого на восемь полусезонов, во-вторых, руководствовались некоторым принципом "взаимодополнения" внутри сезона. (Кстати, 360 (число дней в календаре из 12 месяцев по 30 дней) = 8 (число полусезонов) * 45; ср. значения сумм пар строк в таблице номеров выше).
Самой простой и естественной системой счёта является десятичная. Именно она применялась и применяется у большинства народов мира. Вместе с тем, в ряде древних культур Запада и Востока использовалась более сложная 60-чная система счисления.
60-чная система применялась в шумеро-вавилонской математике и астрономии. Вероятно, она имелась у шумеров ещё до их переселения в Южное Двуречье, так как её использование восходит к наиболее раннему этапу их культуры и так как аккадцы, соседи шумеров, использовали 10-чную систему.
60-чная система применялась шумерами и вавилонянами только в математических и астрономических задачах; в хозяйственных задачах использовалась 10-чная система. Это говорит о том, что её введение было связано со счётом времени, календарём. На связь 60-чной системы с исчислением времени указывают также некоторые "нумерологические" построения древнего Вавилона. Например, число 60 сопоставлялось богу неба Ану; из степеней 60 составлялись различные варианты Великого года – цикла светил.
Из Вавилона 60-чная система перешла в древнюю Грецию, где также применялась для исчисления времени. Этот счёт распространился в Европе.
12- и 60-чные системы счёта, вероятно, применялись в культуре долины Инда.
В арийской индийской культуре счет был 10-чным, но различные варианты продолжительности космического цикла в Индии были кратны степеням 60.
60-чная система использовалась в ранней культуре Китая; ещё в эпоху Инь, около –XV в.; в календарных целях, для счёта дней. В начале нашей эры она стала использоваться и для счёта лет. Применение 60-чной системы в Китае ограничивалось счётом времени; в древнекитайской математике, в отличие от математики Шумера, применялась 10-чная система. Возможно, это было обусловлено тем, что китайская математика меньше применялась в астрономии, чем вавилонская.
Происхождение 60-счёта. 60-чный счёт может рассматриваться как комбинация 10 (или 5)- и 12-чного. В Китае календарная 60-чная система счисления явным образом возникла из соединения 10- и 12-чной систем, притом соотносимых с Солнцем и Луной соответственно: счёт дней велся по 10 солнцам и 12 лунам.
Использование для счёта времени 60 (=5*12) -чного исчисления, возможно, было результатом создания солнечно- лунного календаря.
Солнечно-лунный календарь, ориентирующий земледельческую деятельность в соответствии с движением Солнца, сезонами, а религиозные обряды (праздники, жертвоприношения) – в соответствии с Луной, имелся в древней Индии, Шумере, Вавилоне, Греции. Он перешёл в более поздние культуры: эллинистическую, арабоязычную и другие. Бируни, знаток календарей разных стран, писал: "Сабии, харранцы, израильтяне выводят год из движения Солнца, а месяцы из движения Луны, чтобы их праздники приходились на лунный календарь"[9].
Хотя в Шумере-Вавилоне, в отличие от Китая, связь 60-чной системы счёта с солнечно-лунным календарем не была зафиксирована, но использование шумерами и вавилонянами для хозяйственной деятельности 10-чной системы, а для математической и астрономической – 60-чной напоминает использование солнечного календаря для земледелия, а лунного – для религиозных обрядов. Поэтому можно полагать, что причиной введения 60-чной системы у шумеров тоже было, как и у древних китайцев, комбинирование 10- и 12-чной систем, обусловленное одновременным использованием солнечного и лунного календарей.
Поскольку в сохранившихся клинописных табличках 12-чная система счёта не была отмечена (в отличие от древнекитайских источников), то комбинирование 10- и 12-чной систем счисления для астрономических целей было произведено шумерами/ халдеями, скорее всего, ещё до их переселения в Месопотамию; либо же имелось в некотором общем (для Китая и Шумера-Вавилона) первоисточнике культуры, фрагменты которого (12-чный счёт) лучше сохранились в Китае, чем в Вавилоне.
Магические квадраты (ранняя история)
Время и место появления простейшего магического квадрата, порядка 3*3 (рис. 1а), не определено. Сведений о знакомстве с ним в древнем Вавилоне или античной Греции нет. Косвенным аргументом, что магический квадрат порядка 3*3 знали в эллинистическом мире является ссылка на него в арабоязычной рукописи VIII в. (см. далее). В трактате неопифагорейца Теона Смирнского (+II в.) был приведен псевдомагический квадрат 3*3 (рис. 1б).
Известен магический квадрат порядка 3*3, записанный рунами. Квадрат был обнаружен в книге "Тhe Origin оf Tree Worship", относимой к 1888 году, касающейся ритуалов друидов; он имел вид (рунического) заклинания. После перевода обнаружилось, что "заклинание" является магическим квадратом (рис. 2 а-г). Время возникновение этого квадрата также не определено; историки условно относят его к +III - +V вв. Квадрат, очевидно, был составлен из двух более простых магических квадратов. Весьма примечательной особенностью данного квадрата является то, что при замене (рунических) названий чисел на количество рун в этих названиях получался новый магический квадрат!! (эквивалентный стандартному, только начинающийся с числа 3). В центре этого квадрата вместо 15 оказывалось число 7 – поскольку название числа 15 состояло из 7 рун. (В современном английском языке число 15 также записывается с помощью 7 букв). Наконец, при замене чисел исходного квадрата на сумму их цифр опять получался магический квадрат; в центре которого находилось число 6. Уникальность этих свойств рунического квадрата, в частности связь в нём числе 15 и 7, известная по древним культурам (например, с Иштар, Аполлоном связывались числа и 15 и 7) является аргументом в пользу его оригинальности или даже первообразности для других.
Магический квадрат порядка 3*3 был известен в Китае, где он назывался ло шу, "числа из реки Ло" – по псевдоисторическим легендам мифический культурный герой Фу Си увидел его на спине черепахи, вышедшей из реки Ло. Однако в датированных китайских документах этот квадрат зафиксирован лишь в эпоху Сун (рис. 3), а общее положение о вторичности китайской цивилизации предполагает импорт в неё таких, не связанных с предшествовавшим развитием и не нужных для практики объектов из главных цивилизационных центров. Ло-шу стал популярен в китайской культуре: строились его отображения на макрокосм (порождение сторон света/ мира в соответствие с порядком чисел в ло-шу); на микрокосм (строение тела) и так далее. "Этот простой магический квадрат имел необычную способность представлять основные концепции китайской мысли... ключ к пониманию китайской религии и философии… основа китайской нумерологии"[10].
На тибетских средневековых гадательно-астрологических картах встречался магический квадрат 3*3 (рис. 4). Он изображался там на спине черепахи, в сочетании с 12- чным циклом; триграммами и прочей "китайской спецификой" – что говорит о его трансляции из Китая.
Лучше датированные сведения о магическом квадрате порядка 3*3 относятся к миру арабоязычной культуры, где он впервые появился в рукописи конца VIII века, приписывавшейся алхимику Джабиру ибн Хайану (Геберу). В тексте рукописи автором этого квадрата был назван неопифагореец Аполлоний Тианский, живший в +I веке[11].
Вскоре в арабоязычном мире стали известны и магические квадраты высших порядков. Сочинение о магических квадратах написал сирийский математик Сабит ибн Корра ал Харрани (835 - 901 гг.). Квадраты порядков 3 - 9 были приведены в энциклопедии "Братьев Чиcтоты" – серии трактатов, написанных во 2-ой половине X века.
Магические квадраты в арабоязычном мире использовались в астральной магии, т.е. как талисманы: Сатурну был соотнесён квадрат 3*3, Юпитеру – 4*4,… Луне – 9*9. Квадрат 3*3, соотносившийся с Сатурном, применялся также как талисман "для облегчения родов".
В Индии (Кханджурахо) был обнаружен совершенный магический квадрат[12] порядка 4*4, относимый предположительно к VIII-IX вв[13].
В XII веке в Испании сочинение о магических квадратах написал р. Абрахам бен Эзра (1092 - 1167 гг.), занимавшийся астрологией.
По некоторым сообщениям, магический квадрат 3*3 был изображен на коронационной мантии сицилийского короля Рожера II (XII в.)
Ряд магических квадратов приводился в работе византийского учёного XIV века Мануэля Мосхопулоса. Мосхопулос описал метод построения квадратов нечётного порядка, названный им "индийским"; также привёл (без вывода) пример совершенного магического квадрата 4*4, совпадавшего с индийским. Возможно, Мосхопулос следовал работе персидских учёных: аналогичные примеры имелись в анонимной персидской рукописи 1212 года[14].
Самым ранним латиноязычным сочинением, где был приведен список магических квадратов порядков 3 - 9, является трактат Агриппы "Об оккультной философии" (1508- 32 гг.). Агриппа, следуя традиции арабоязычной магии, соотносил с этими квадратами планеты, то есть, применял их как талисманы для астральной магии (рис. 5). Поскольку в своей книге он приводил рядом с квадратами, написанными современными цифрами, аналогичные, написанные еврейскими цифрами (буквами), то, видимо, он заимствовал их частично из книг (испанских) евреев, возможно, того же бен Эзры[15].
Художник Альбрехт Дюрер (1471 - 1527/8 гг.) на своей картине "Меланхолия" изобразил совершенный магический квадрат, увязав его с годом создания картины (1514 г.); см. рис. 6.
Магические квадраты приводил в свои работах Штифель (1487 - 1567 гг.), немецкий математик, автор сочинений "Курс арифметики" (1544 г.), "Немецкая арифметика" (1545 г.), профессор университета Иены; одновременно священник- протестант и каббалист.
В XVIII веке Симон де ла Любер, посланник Франции в Сиаме, привёз в Европу метод построения магических квадратов, названный им "сиамским".
В дальнейшем задачи на построение магических квадратов стали популярным разделом занимательной математики.
Рис. 1а. Магический квадрат третьего порядка.
4 9 2
3 5 7
8 1 6
Рис. 1б. Псевдомагический квадрат Теона Смирнского
1 2 3
4 5 6
7 8 9
Рис.2а. "Друидический квадрат" в буквенной записи (англ.).
Five twenty two eighteen
twenty eight fifteen two
twelve eight twenty five
Рис.2б. "Друидический" магический квадрат в числовой записи.
5 22 18 0 20 10 5 2 8
28 15 2 = 20 10 0 + 8 5 2
12 8 25 10 0 20 2 8 5
Рис.2в-г. "Друидический" квадрат.
4 9 8 5 4 9
11 7 3 10 6 2
6 5 10 3 8 7
в) число букв в исходном г) сумма цифр в исходном
Рис. 3. Изображение ло-шу в китайском трактате эпохи Мин (XIV в.).
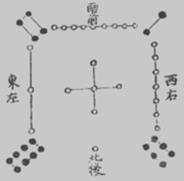
Рис. 4. Тибетские магические квадраты 3*3, эквивалентные ло-шу
(изображены в круге на черепахе, тибетскими цифрами)
Рис. 5. Магические квадраты в сочинении Агриппы "Оккультная философия".
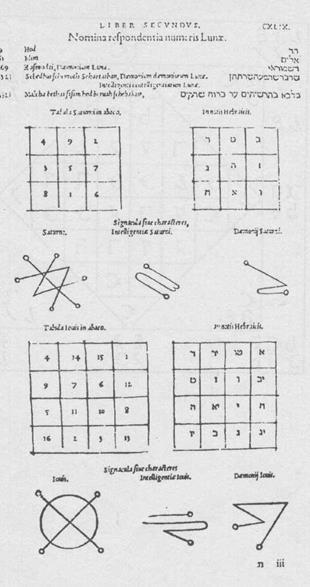
Рис. 6. Магический квадрат на картине А. Дюрера "Меланхолия"

В нижней строке выделены числа 15 и 14 – год создания картины.