Спиральные симметрии в природе, науке, искусстве
Введение. Спирали, симметрии, закономерности
Природа
галактики; вихри, водовороты; частицы в силовых полях
филлотаксис (расположение листьев); раковины моллюсков; рога животных
Искусство
спирали в творчестве Леонардо да Винчи
спирали в творчестве Альбрехта Дюрера
Математика
спираль Архимеда; винтовые линии
Физика
теория вихрей (основные понятия и свойства)
изучение спиральных структур в физике (исторический обзор)
Биология
филлотаксис (основные термины, факты, модели)
изучение спиральных структур в биологии (исторический обзор)
Спиральные симметрии симметрии в природе, искусстве, науке
Введение. Спирали, симметрии, закономерности.
Спиральное, или вихревое движение часто встречается в Природе. От центров галактик отходят спиральные рукава. По спиралям- вихрям движутся частицы воды или воздуха в смерчах, торнадо, водоворотах. По спиральным кривым движутся заряжённые частицы в магнитных полях. По спиралям растут листья деревьев и лепестки цветов, раковины моллюсков.
В живой природе часто встречаются логарифмические спирали, которые поэтому могут быть даже названы линиями жизни (ср. название книги Cook T. "The curves of life", 1915).

Логарифмические спирали вызывают впечатление симметричности. Они и в самом деле симметричны – переходят в себя при некоторых преобразованиях: повернув такую спираль на определённый угол и совершив над ней преобразование подобия с определённый коэффициентом, мы получим ту же спираль. Таким образом, если равномерно поворачивать эту спираль вокруг её центра, то она будет как бы равномерно увеличиваться – "расти", оставаясь подобной самой себе. Это свойство логарифмических спиралей сближает её с процессами, происходящими в живой (и даже неживой – см. напр. ниже фотографии галактик – природе.
Преобразования поворота с растяжением вокруг фиксированной точки О образуют, очевидно, группу. Их можно назвать преобразованиями роста, поскольку они представляют процессы роста живых объектов, когда эти объекты увеличиваются в размерах, оставаясь подобным самим себе. На некотором установившемся этапе роста такие преобразования происходят относительно равномерно; в начале- особой точке рост объектов неравномерен и, вероятно, следует (до выхода на устойчивый режим) экспоненциальному закону, а в конце – также экспоненциально угасает. К такому поведению наиболее близок график логистической функции.
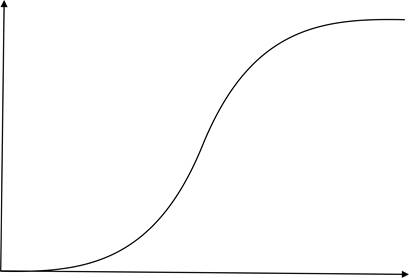
Обычные (без растяжения) повороты вокруг О также образуют, очевидно, группу. Их можно рассматривать как преобразования "нулевого роста", производимые в пространстве объектом, когда его развитие- рост уже прекратилось.
Наличие группы симметрии для некоторого класса объектов в природе означает и наличие (математического) закона, которому подчиняется поведение таких объектов. Или, применяя выражение Плотина, переформулированное Гейзенбергом: в таких объектах для исследователя начинает "просвечивать" (математическая) идея. Одним из основных методов современной фундаментальной физике является изучение симметрий и связанных с ними законов сохранения- инвариантности.
Природа
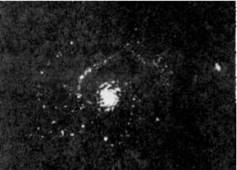





Вихрь-тайфун (вид сверху) Пылевой вихрь на Марсе





Мальмстрем



Треки a-частиц в магнитном Треки электрона Треки заряжённых частиц
поле (фото 1923 г.) в камере Вильсона
Филлотаксис (расположение листьев)


Подсолнечник


Сосновые шишки

Кедр ливанский


Кактус Маммиллярия


Sempervivum

Эхеверия агавовая


Nautilus (кораблик), головоногий моллюск


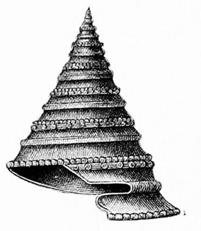
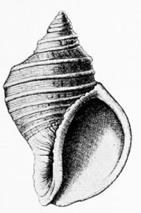
Dolium galea морской брюхоногий моллюск
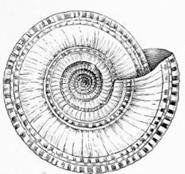

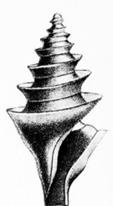
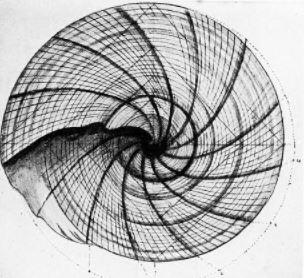
Solarium


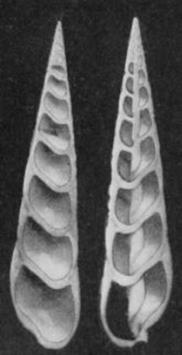
Аммониты





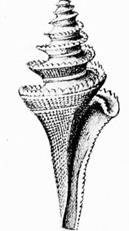


Рога животных


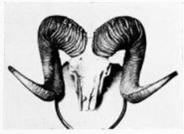



Искусство
Изображения спиралей с древнейших времён часто встречались в искусстве. Спиральные рисунки были найдены в самых разных культурах и во всех частях света – в Средиземноморье, в Европе, в Азии, на Дальнем Востоке, в Южной и Северной Америках.

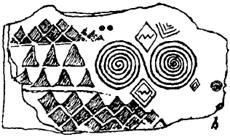
Спирали на доисторических мегалитах Ирландии (Нью-Грейндж)

Готландский камень


Керамика неолитической культуры Триполье (–V тыс.)


Керамика неолитической культуры Яншао (–V тыс.)



Керамика неолитической культуры Лендьел (–IV тыс.)

Критская керамика (–III - –II тыс.)

Двойная спираль на хеттской печати.
Амулеты из Трои.




Спирали на древних амулетах и памятниках Малой Азии.

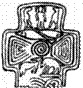
Спирали на древних амулетах и памятниках Британии.
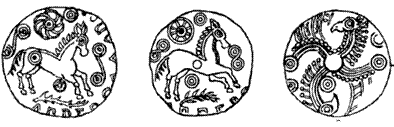
Спирали на древних бриттских монетах.


"Кельтские" спирали
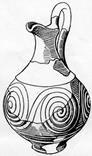

Минойская ваза Этрусская ваза


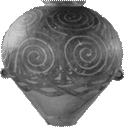
Сосуды из Триполья Китайский сосуд


Спирали на скифском сосуде Алтарь в Центральной Америке
Броши из культуры Гальштат

Спирали на золотом античном галльском диске

Греческая ваза с меандровым (спиралеподобным) узором.

Изображение на греческой вазе около –310 г., из Нолы.

Декоративный фриз Парфенона.
В античной архитектуре, начиная с Древней Греции, спирали изображались на вершинах (капителях) колонн, сделанных в ионическом или коринфском стиле.



Ионический стиль



Коринфский стиль. Колонны коринфского стиля увенчивали спирали, рядом с которыми изображались декоративные листья, напоминающие листья аканта[1].
Представляли спиральное движение и свастики, многочисленные изображения которых также имелись в разных культурах, начиная с древности.



Месопотамские, хеттские спирали-свастики.




Спирали-свастики на древних бриттских памятниках.
Спирали-свастики на амулетах из Трои.

Свастики на "троянском" храме в Лациуме.
Свастики на одеянии финикийской жрицы Солнца.




Спирали-свастики в Индии



Спирали-свастики в культурах Евразии




Спирали-свастики в скифо-сарматском искусстве



Спирали-свастики у славян и на Руси


Традиционные мотивы вышивки и кружев. Вологда


Французская готика, 13 век. Монастырь Сен-Гийем-ле-Дезер; камень (вверху). Нотр Дам, западная дверь; железо (внизу).

Основания статуй в соборе Шартра.

Колонна в часовне Рослин (Шотландия), 15 век, слева.




Замок Блуа.

Замок Вестминстер (Англия). Расписанная палата.

Замок Колчестер (Англия).
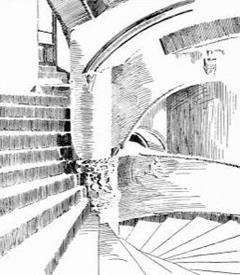
Замок Файви (Шотландия)

Собор св. Павла (Лондон, архитектор Рен, 17 век).

Собор св. Лазаря (Отун, Франция)


Дворец Контарини (Венеция).

Замок в Граце (Австрия).

Замок Хагенфельс (Германия).

Замок Шадау (Швейцария).
Спирали в творчестве Леонардо да Винчи
Спираль как форма, наиболее полно выражающая идею роста и развития, во все времена имела особую притягательную силу для лиц творческих профессий.
Леонардо да Винчи (1452 - 1519 гг.) проявил большой интерес к наблюдениям над Природой, а также к поиску геометрических форм и арифметических закономерностей в ней. Последнее соответствовало духу Итальянского Ренессанса, характеризовавшегося возрождением античных пифагорейских идей об устройстве мира по математическим образцам. Изучая раковины моллюсков, он в своих рисунках правильно изобразил их спиралевидные формы:

а рассматривая строение растений, он одним из первых (после античных натурфилософов) отметил регулярность расположения листьев на них, выражавшуюся в том, что 6-й лист оказывается на стебле ровно над 1-м.
Свои наблюдения и исследования Леонардо да Винчи применял в художественной работе – в живописи, скульптуре, архитектуре, инженерном деле.
Наброски и картины Леонардо да Винчи, имеющиеся в Виндзорской коллекции, показывают его особый интерес к спиралям:
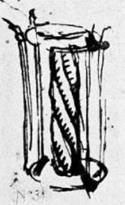
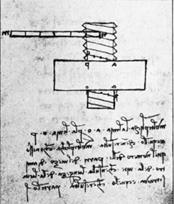

Леонардо да Винчи. 1, 2- винты; 3- воздушный винт. Наброски.

Леонардо да Винчи. Вихри пыли и дыма. Набросок.


Леонардо да Винчи. Воды Потопа и вихри в них. Наброски.


Леонардо да Винчи. Леда. Набросок.

Бюст (на барельефе) Сципиона Африканского.
Леонардо да Винчи (предположительно).
Историки архитектуры считают, что Леонардо да Винчи принимал участие в проектирование замка Шамбор, с его искусно сконструированной винтовой (= спиральной) лестницей. Само строительство замка началось в 1519 году, через несколько месяцев после смерти итальянского мастера.


Замок Шамбор (Франция, 16 век). Дизайн Леонардо да Винчи (предположительно).
Т. Кук полагал, что Леонардо да Винчи участвовал также в строительстве или проектировании замка Блуа (и винтовой лестницы там). Прямых свидетельств этого нет (архитекторами замка Блуа считаются Жак Сурдо (Sourdeau) ( - 1530? гг.) и Симон Гишар), но Т. Кук привёл несколько косвенных аргументов[2]:
1) Прибыв во Францию в 1516 г. по приглашению короля Франциска I (правление 1515- 47 гг.), Леонардо да Винчи, занял должность "первого королевского художника, инженера и архитектора". Ранее, в 1506- 12 гг., когда он находился в Милане (которым тогда управляли французы), он уже выполнял работы для французского короля (в те годы это был Людовик XII).
2) Во Франции да Винчи жил в представленном ему Франциском I поместье в Кло-Люсе, неподалёку от реки Луары, близ которой расположен и замок Блуа.
3) С 1516 г. начались выплаты из королевской казны на достройку замка в Блуа. Известно, что после 1519 г., когда Леонардо не стало, архитектором замка в Блуа был Жак Сурдо. Однако неясно, кто занимался постройкой замка в промежутке 1516- 19 гг. Между тем, с 1516 до 1519 гг. Леонардо да Винчи официально являлся королевским художником, инженером и архитектором.
4) Формы лестницы в Блуа напоминают спирали раковин моллюсков, изучением которых занимался да Винчи.
5) В его записных книжках есть проекты винтовых лестниц.
Все эти косвенные аргументы свидетельствуют о возможном участии Леонардо да Винчи в проектировании или постройке замка Блуа в 1516- 19 гг., в те годы, когда была построена винтовая лестница там.
Спирали в творчестве Альбрехта Дюрера
Художник, гравёр и математик Альбрехт Дюрер (1471 - 1528 гг.) из Нюрнберга был младшим современником Леонардо да Винчи. Как и да Винчи, и также в соответствии с духом Ренессанса, он проявлял большой интерес к экспериментальным наблюдениям Природы и к исследованиям в области математики, результаты которых он применял в своём творчестве.
В 1525 г. в Нюрнберге вышел трактат Дюрера "Рассуждения об измерениях циркулем и линейкой" (Unterweisung der Messung mit dem Zirkel und Richtscheit), основной темой которого было применение математики к художественной практике. Автор описал методы построения ряда фигур, включая многочисленные спирали. Это была первая книга того времени по математике, написанная на немецком языке – что делало её доступной гораздо более широкому кругу читателей, чем издававшиеся ранее преимущественно на латинском и греческом языках работы Эвклида и других античных и средневековых учёных. (Чтобы точнее представить себе значение этой работы в математическом отношении для эпохи Ренессанса, следует учесть, что ключевой трактат "Начала" Эвклида был издан всего за 40 лет до работы Дюрера, притом на латыни и в Венеции. На национальных языках первым стало издание перевода "Начал" на итальянский, сделанного Лукой Пачиоли в 1509 г. В центральной Европе "Начала" были изданы впервые только в 1533 г. С. Гринеем, притом на греческом языке).
В первой части "Рассуждения" Дюрер сообщил своим читателям, что он поставил целью этой работы дать основу тем, кто намерен заниматься живописью, и эту основу он видит в геометрии, в "измерениях циркулем и линейкой", принципы которых заложил "наимудрейший Эвклид". Повторив и проиллюстрировав определения точек и линий из "Начал", Дюрер далее сказал, что он делит все линии на три вида: прямые, окружности, и кривые (Schlangen lini - змеевидные):

Рис. Д1.
Кривыми Дюрер в 1-й части своего трактата, в основном, и занимался. Среди них были спираль Архимеда, логарифмическая спираль, конхоида, эпициклоида, эпитрохоида, гипотрохоида, улитка Паскаля. Большинство составляли спирали ("улиточные линии" - Schnecken lini) и винтовые линии (Schrauben lini). Для одних кривых он приводил методы их вычерчивания с помощью циркуля и линейки, другие строил с помощью наложения сетки, или от руки. Среди первых были спирали ионического стиля (см. рис. Д2).
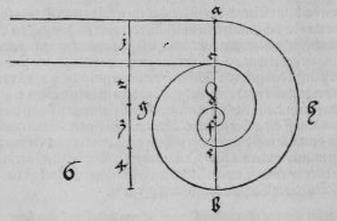
Рис. Д2. (Числа вне спирали – это номер рисунка в книге).
Эту спираль Дюрер строил с помощью циркуля и линейки следующим образом. Разделим отрезок аb на четыре равные части точками с, d, e, затем отрезок de точкой f на две равные части, и напишем слева от отрезка аb букву g, справа – h. Затем, с помощью циркуля строим дугу окружности с центром в d и радиусом dа, на стороне h, до точки b. Далее построения аналогичны.
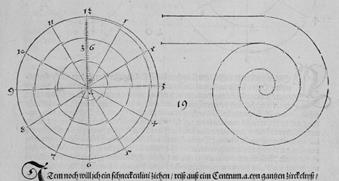
Рис. Д3.
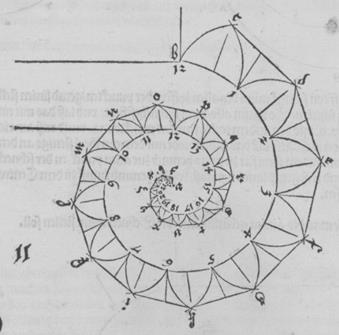
Рис. Д4.
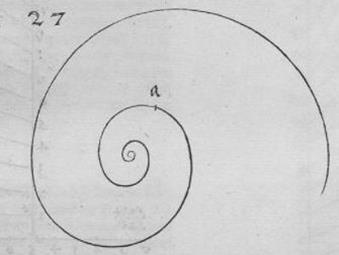
Рис. Д5. "Логарифмическая спираль" (вечная линия - ewige lini). Дюрер строил её вручную, однако, очевидным образом "следуя натуральным объектам" (Т. Кук, цит. соч.).
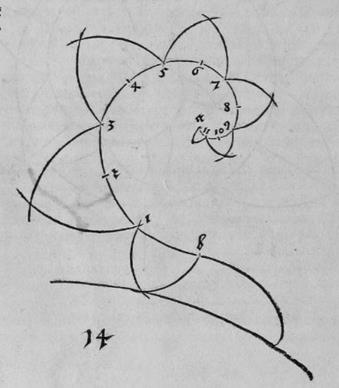
Рис. Д6. Спиралевидное растение.
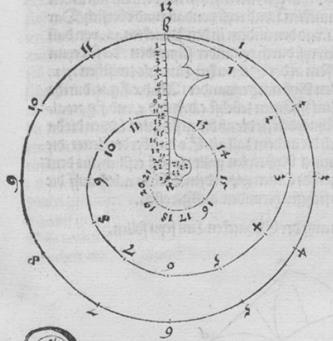
Рис. Д7.
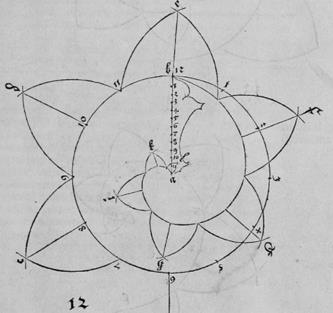
Рис. Д8.
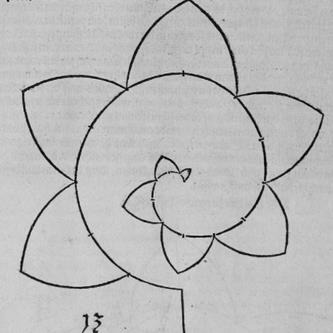
Рис. Д9. Навершие т.н. "посоха епископа".
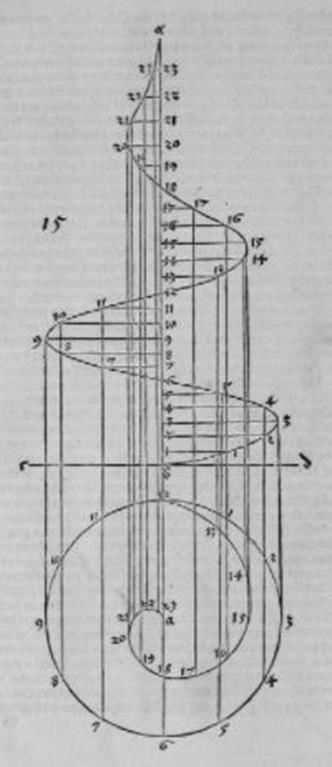
Рис. Д10. Расчёт размеров конической спирали по плоской.
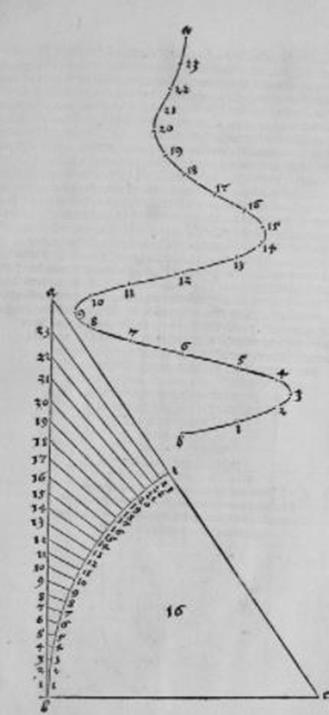
Рис. Д11.
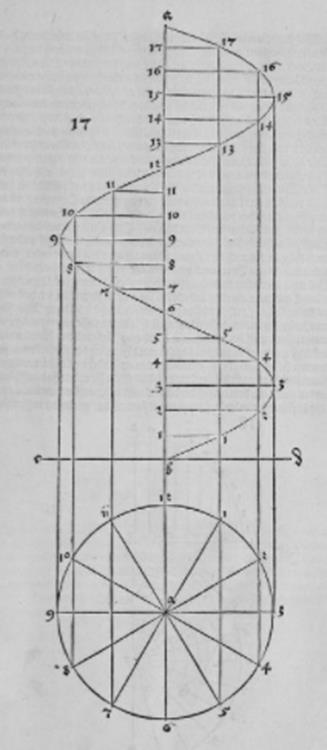
Рис. Д12.
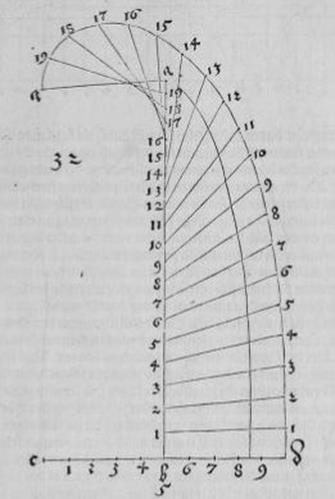 .
.
Рис. Д13.
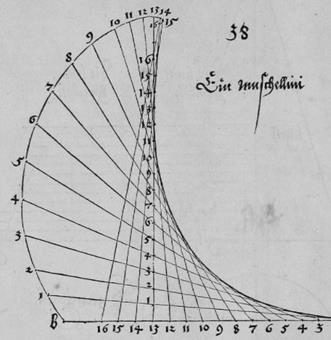
Рис. Д14.
Логарифмическая спираль – это кривая, задаваемая в полярных координатах соотношением
r(j) = ebj + a = Aebj
где r – длина радиус-вектора точки, j – угол поворота радиус-вектора относительно полярной оси координат; b и a – некоторые параметры.
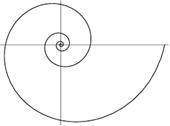
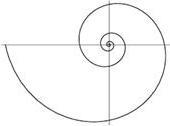
Рис. 1. b > 0. Рис. 2. b < 0.
Знак параметра b определяет, в каком направлении закручивается спираль. Если b > 0 то спираль закручивается против часовой стрелке (рис. 1). Если b < 0 то спираль закручивается по часовой стрелке (рис. 2).
Величина параметра b определяет плотность витков спирали: при уменьшении b расстояние между соседними витками спирали уменьшается.
Если b = 0 то логарифмическая спираль вырождается в окружность (рис 3). Если b ® ¥ то логарифмическая спираль стремится к прямой (рис 4).


Рис. 3. b = 0. Рис. 4. b ® ¥
Параметр a определяет поворот спирали вокруг полюса О; при его изменении спираль просто вращается вокруг О.
1). Главным свойством логарифмической спирали является самоподобие: поворот её на любой угол b вокруг полюса О эквивалентен её преобразованию подобия с некоторым коэффициентом p.
Связь между коэффициентом подобия p и углом поворота b выражается через b:
p = ebb
Другое выражение этого свойства – "рост" спирали эквивалентен её преобразованию подобия и повороту; т.е. её части S1 и S2, образованные "обрезанием" спирали по углам j1 и j2, таковы, что S1 = повёрнутое на некоторый угол и увеличенное с некоторым коэффициентом S2. Или иначе: с увеличением числа витков логарифмической спирали их форма остаётся неизменной (подобной).
При повороте на 2pn спираль совпадёт сама с собой, а коэффициент подобия при этом будет
p = eb2pn
Т.о. при увеличении спирали в eb2pn раз она совпадёт сама с собой.
2). Угол a, составляемый касательной в любой точке логарифмической спирали с радиус-вектором точки касания, постоянен (рис. 5).
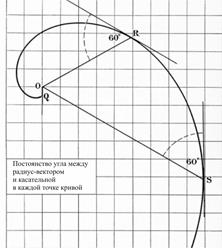
Рис. 5.
Из-за этого свойства логарифмическую спираль называют также равноугольной.
Это свойство является характеристическим – кривая, удовлетворяющая ему, представляет собой логарифмическую спираль.
Угол касания a связан с параметром спирали b соотношением b = ctg a.
Если угол касания a = 90о, то логарифмическая спираль представляет собой окружность.
3). Если угол радиус-вектора возрастает/ убывает в арифметической прогрессии, то величина радиус-вектора возрастает/ убывает в геометрической прогрессии (рис. 6).
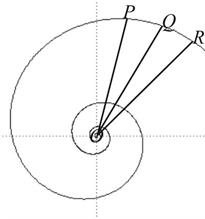
Рис. 6. Если угол ROQ равен углу QOP, то OR/OQ = OQ/OP.
Это свойство также является характеристическим.
3'). В частности, при повороте на 2p длина радиус-вектора для любой точки увеличивается в одно и то же число раз, |r(j+2p)| = k|r(j)|.
k – ширина завитков спирали; называется коэффициент роста.
k связан с параметром спирали b соотношением: k = e2pb
k связан с углом касания a соотношением: k = e2pctga.
3''). Любые два треугольника, с центрами в полюсе О и вершинами в точках спирали, такие, что их углы в О равны, будут подобны между собой.
4). Если прямая равномерно вращается вокруг точки О, и на ней движется точка со скоростью, пропорциональной расстоянию от О, то кривая, образуемая движением этой точки представляет собой логарифмическую спираль.
5). Длина дуги логарифмической спирали между углами j1 и j2 составляет
|(r(j2) - r(j1)| (Ö(b2+1))/b = |(r(j2) - r(j1)|/cos a
Полная длина спирали (при b>0) между –¥ и j составляет .
S(j) = r(j) (Ö(b2+1))/b = r(j)/cos a
5'). Уравнение логарифмической спирали, выраженное через длину дуги:
r(s) = s*cos a
Т.о. радиус-вектор линейно зависит от длины дуги.
6). Центр кривизны логарифмической спирали в данной точке находится на пересечении нормали и перпендикуляра к ней, проведённого из полюса.
Радиус кривизны логарифмической спирали составляет .
R(j) = r(j)/sina
Радиус кривизны логарифмической спирали, выраженный через длину дуги:
R(s) = s*ctg a
Т.о. радиус кривизны линейно зависит от длины дуги.
6'). Длина l отрезка касательной от точки касания до перпендикуляра, опущенного из полюса О на касательную:
l = r(j)/ cos a = длина дуги до этой точки
7). Локсодромы на сфере при стереографической проекции сферы на плоскость переходят в логарифмические спирали. (Локсодромами называются линии, пересекающие меридианы под постоянным углом (рис. 7)).
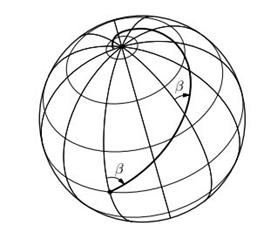
Рис. 7.
8). Эволютой логарифмической спирали является та же логарифмическая спираль, повёрнутая на некоторый угол q (рис. 8). (Эволютой к данной кривой называется г.м.т. центров кривизны этой кривой).

Рис. 8.
8'). Если дуга логарифмической спирали катится без скольжения по прямой, то центры кривизны её точек касания движутся по прямой.
9). Эвольвентой логарифмической спирали является та же логарифмическая спираль повёрнутая на некоторый угол (рис. 9). (Эвольвентой (инволютой) к данной кривой называется кривая, нормаль в каждой точке которой является касательной к исходной кривой. Если кривая S1 является эволютой кривой S2, то S2 является эвольвентой S1).
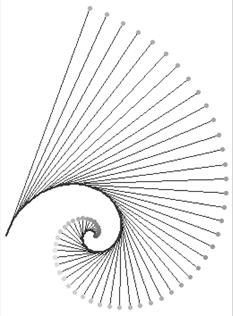
Рис 9.
9'). Если намотать на логарифмическую спираль нить, концом которой служит некоторая точка О', а затем начать разматывать эту нить, то её конец опишет линию конгруэнтную исходной спирали.
10). Каустикой лучей с источником света в центре логарифмической спирали, отражённых от этой спирали, является такая же логарифмическая спираль (рис. 10). (Каустикой называется огибающая семейства лучей).

Рис. 10.
10'). Будем опускать из полюса (центра координат) О перпендикуляры на все касательные к логарифмической спирали. Получающееся геометрическое место точек будет такой же спиралью, только повёрнутой на некоторый угол (рис. 10').
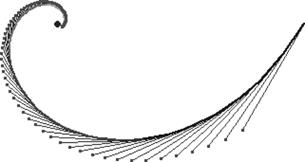
Рис. 10'.
11). Образом логарифмической спирали при инверсии относительно окружности с центром в полюсе является логарифмическая спираль (рис. 11).
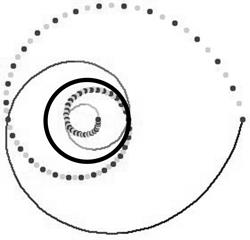
Рис. 11.
12). Если к равнобедренным треугольникам, прямоугольникам или квадратам присоединять их гномоны, то вершины получающихся самоподобных фигур будут лежать на логарифмической спирали (рис. 12' и 12'').
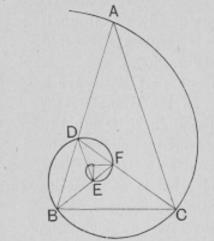
Рис. 12'.
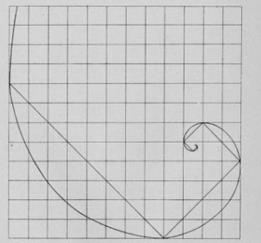
Рис. 12''.
Золотое сечение и спиральность. Золотое сечение, т.е. отношение a/b такое, что a/b=(a+b)/a (» 1,618), помимо других своих многочисленных замечательных качеств, имеет и некоторую связь со спиральностью; а именно, если к прямоугольнику A со сторонами a и b добавить его гномон G1 (т.е. фигуру, дополняющую данную до подобной ей), который, как нетрудно видеть из свойств золотого сечения, окажется в этом случае квадратом, а затем этот процесс продолжить, то центры образовавшихся квадратов будут лежать на спирали.
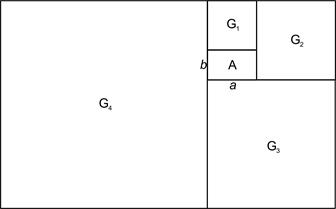
Рис. 12'''.
13). Пусть на логарифмической спирали S с полюсом в O дана последовательность точек {An}, таких, что для всех n угол An+1OAn = AnOAn-1. Будем называть такую последовательность (а также исходную спираль) генетической, а угол An+1OAn – её углом расхождения.
Пусть точки Bnи Cn являются ближайшими сверху к An, слева и справа соответственно. Тогда последовательности {Bn}и {Cn} также лежат на логарифмических спиралях SB и SC с полюсами в той же точке O, притом закрученных в разные стороны.
Такие последовательности {Bn}и {Cn} (и соответствующие спирали SB и SC) будем называть парастихами.
14). Отобразим плоскости p с полярными координатами (O, L)на плоскость p' с декартовыми координатами O'XY по правилу (j, r) ® (j (mod 2p), ln r). Будем называть его отображением Браве. Тогда логарифмические спирали r(j) = ebj + a в плоскости p переходят в отрезки прямых в плоскости p', параллельные между собой. Параметр b спирали переходит в коэффициент наклона отрезка к оси OX. Это отображение является конформным.
14'). Пусть на логарифмической спирали S с полюсом в O и уравнением r(j) = ebj + a, лежащей в плоскости p, дана последовательность точек {An}, таких, что для всех n угол An+1OAn = AnOAn-1. При отображение Браве плоскости p на плоскость p' последовательность {An} точек на спирали S переходит в ромбическую решётку в плоскости p'. Парастихи {Bn}и {Cn}переходят в подрешётки этой решётки
15). Пусть дана последовательность {An} точек на плоскости, конечная или бесконечная, такая, что для всех n угол An+1OAn = AnOAn-1 = q = const, а r(O, An+1)/r(O, An) = k = const. Тогда {An} лежит на логарифмической спирали, притом её уравнение r(j) = Aebj, где b = lnk/q, а значение A определяется из условия ln(OAn) (=lnAebj = lnA + lnebj = lnA + bj) = lnA + bjn = lnA + b (LOAn + 2pk).
16). Пусть во всех вершинах некоторого правильного многоугольника сидит по одному насекомому. Пусть каждое начинает ползти по направлению к своему правому соседу с постоянной скоростью (рис. 13 для квадрата; рис.14 для шестиугольника ). Тогда их траектории представляют собой логарифмические спирали.
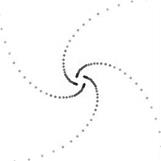
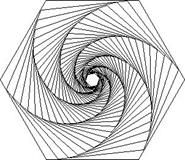
Рис. 13. Рис. 14.
17).
Впервые дал описание логарифмической спирали немецкий художник и математик Альбрехт Дюрер (1471 - 1528 гг.) приводивший её в своём трактате 1525 года "Руководство к измерению[3] циркулем и линейкой" (рис. 15). Он назвал её "вечной линией" (ewige lini).

Рис. 15.
Хотя Альбрехт Дюрер больше известен как художник, но он был и видным математиком; его вышеупомянутый трактат являлся одним из ранних немецких сочинений по математике. В нём Дюрер дал описания геометрических фигур и способов их построения (имея в виду применение в художественной практике). Среди этих фигур были и разные виды спиралей, которых Дюрер называл "улиточными кривыми" (Schneckenlinien), (пример: рис. 16).
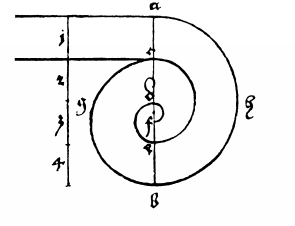
Рис. 16.
Дюрер также занимался теорией перспективы, и он является одним из основателей начертательной геометрии.
Логарифмическую спираль изучал английский математик Томас Хариот (1560 - 1621 гг.); она появилась в его работах как проекция локсодромы на плоскость (см. далее Задачи). Впрочем, Хариот почти не публиковал результатов своих научных исследований.
Через 100 лет после Дюрера логарифмической спиралью, точнее, кривой, у которой в каждой точке касательная образует с радиус-вектором всегда один и тот же угол, подобно окружности, заинтересовался Декарт (1596 - 1650 гг.). Он описал её в своём сообщении 1638 г. к Мерсенну. Декарт фактически нашёл её уравнение в полярных координатах. Он также вычислил длину её дуги.
Почти одновременном с Декартом и независимо от него логарифмическую спираль изучал итальянский математик Торричелли (1608- 47 гг.).
Интерес к логарифмической спирали проявил швейцарский математик Якоб Бернулли (1655 - 1705 гг.), называвший её, из-за свойства самоподобия, "удивительной кривой".
Название логарифмическая спираль ввёл в 1704 г. французский математик и механик П. Вариньон (1654 - 1722 гг.), основываясь на том её свойстве, что угол между радиус-векторами её точек пропорционален логарифму их отношений.
В XIX веке, в связи с открытием спиральности форм многих живых организмов (растений, раковин моллюсков), логарифмическая спираль стала популярной среди биологов. Английский математик Генри Мосли (1801- 72 гг.) показал, что раковины моллюсков Nautilus образуют почти точные логарифмические спирали (при этом он использовал характеристическое свойство 3', см. выше); потом он обобщил это утверждение для аммонитов и моллюсков класса Gastropod (брюхоногие, улитки). После Мосли такие же вычисления для раковин разных видов моллюсков проводили немецкий натуралист К.Ф. Науман (1797 - 1873 гг.) и другие учёные. Были найдены характеристические коэффициенты геометрических прогрессий для радиус-векторов и, соответственно, характеристические углы касательных к спиралям раковин. Сходные исследования проводились в XIX в. и для филлотаксиса (расположения листьев растений).
Архимед (–III в.) рассматривал кривую, получающуюся при равномерном движении точки одновременно по окружности и лучу, выходящему из центра этой окружности. Такое движение порождает спираль.
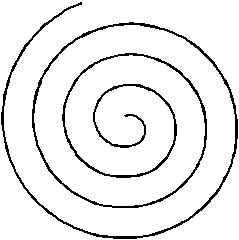
Уравнение спирали Архимеда в полярных координатах ρ = kφ.
Свойства спирали Архимеда:
1). Длина всех завитков одинакова.
2). Спирали, полученные при движении точки со скоростями v1, v2 подобны с коэффициентом v1/v2.
3) Пусть Р – точка пересечения касательной к спирали в некоторой точке А и перпендикуляра, восставленного к отрезку ОА в точке О. Тогда длина отрезка ОР равна длине окружности с радиусом ОА.
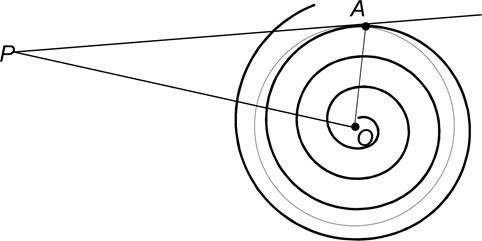
Из-за этого свойства спираль Архимеда можно применять для решения задачи квадратуры круга.
Цилиндрическая винтовая линия задаётся в декартовых координатах уравнениями:
x(t) = Rcost; y(t) = Rsint; z(t) = b t
Она расположена на цилиндре с радиусом R и составляет во всех точках одинаковые углы с образующими цилиндра.
Проекция цилиндрической винтовой линии на плоскость, перпендикулярную оси цилиндра, представляет собой окружность.
Коническая винтовая линия задаётся в декартовых координатах уравнениями:
x(t) = ktcost; y(t) = ktsint; z(t) = bt
Она расположена на круговом конусе. Параметры k и b связаны с углом развёртки конуса a соотношением
a = arctg (b/k)
Коническая винтовая линия, в отличие от цилиндрической, не составляет во всех точках одинаковые углы с образующими конуса.
Проекция конической винтовой линии на плоскость, перпендикулярную оси конуса, представляет собой спираль Архимеда.
Логарифмическая винтовая (или цилиндроконическая) линия задаётся в декартовых координатах уравнениями:
x(t) = Аekt cost; y(t) = Аekt sint; z(t) = bekt
Логарифмическая винтовая линия лежит на некотором круговом конусе, составляет во всех точках одинаковые углы с образующими этого конуса, и её проекция на плоскость, перпендикулярную оси конуса, представляет собой логарифмическая спираль.
Физика
Теория вихрей (основные понятия и свойства)
Пусть в области W Ì R3 имеется некоторое дифференцируемое векторное поле, задаваемое в декартовой системе координат OXYZ как u(x, y, z). (Его далее можно интерпретировать как поле скоростей движущейся сплошной среды (жидкости, газа, ,…) в некоторый момент времени t). Вихрем u(x, y, z) называется векторное поле rot u = (¶u/¶z – ¶u/¶y, ¶u/¶y – ¶u/¶x, ¶u/¶x – ¶u/¶y).
Механическая смысл rot: пусть б.м. частица вращается в плоскости OXY вокруг оси OZ с угловой скоростью w, и пусть u(x, y, z) – поле её скоростей. Тогда rot u направлен по оси OZ и |rotu| = 2w. Т.е. вихрь равен (удвоенной) мгновенной угловой скорости вращения б.м. элемента среды.
Поле u(x, y, z), такое, что rot u = 0, называется потенциальным, Оно удовлетворяет уравнению Лапласа Du = 0 и для u(x, y ,z) существует скалярная функция j (потенциал) такая, что u = Ñj..
Любое (кусочно-дифференцируемое) векторное поле может быть представлено в виде суммы потенциальной (безвихревой) и соленоидальной (вихревой) компонент: u(x, y, z) = Ñj + rot y.
Завихрeнность идеальной (= невязкой, без внутреннего трения) несжимаемой жидкости имеет динамику:
dw/dt = rot [u. w] (где [u. w] – векторное произведение)
Завихрeнность вязкой несжимаемой жидкости с коэффициентом вязкости (= внутреннего трения) m имеет динамику:
dw/dt = rot [u. w] + mDw
Из этих уравнений можно показать, что в вязкой жидкости со временем происходит диффузия и выравнивание локальных завихрeнностей, т.е. как бы сглаживание вихрей.
Вихревая линия – касательная к которой в каждой точке направлена по вектору вихря; вихревая трубка – множество вихревых линий, проходящих через замкнутую кривую; вихревое кольцо (тороидальный вихрь) – замкнутая вихревая трубка. В идеальной жидкости для них имеют место свойства: 1) сохранение вихрей (вихревых колец); 2) частицы жидкости, расположенные на вихревой линии, при своем перемещении всегда будут принадлежать к той же линии; 3) вихревые линии внутри жидкости либо замкнуты, либо оканчиваются на ее границе.
Изучение спиральных структур в физике (исторический обзор)
XVII - XVIII вв.
вихревая теория тяготения (последователи Декарта)
XIX в.
середина XIX - начало XX вв.
Спиральные движения в природе – вихри в воздухе, на воде – несомненно, обращали на себя внимание людей с древности. Вероятно, они, наряду с чаще встречающимися в обычной жизни спиральными структурами в мире живого, оказали влияние на многочисленные изображения спиралей и близких к ним фигур в искусстве ранних цивилизаций Малой Азии, Ближнего Востока, Средиземноморья.
Древние учёные и философы использовали замечаемые ими вихревые- спиральные движения, в основном, в двух отношениях: 1) для практики – устройства механизмов, действие которых было бы в чём-то подобно этим движениям; 2) для теории – в попытках дать объяснения тем или иным явлениям природы; уподобляя их в чём-то наблюдаемым вихрям.
В античной Греции Левкипп и Демокрит (–V в.) построили основанную на представлениях о вихрях космогонию. Согласно ей, исходно существовала пустота, в которой хаотично двигались атомы. Случайным образом в этом движении стали возникать вихри, из-за чего часть атомов постепенно соединилась в тела; из них более тяжёлые оставались в центре вихрей, а более лёгкие отходили на периферии. В центре одного из таких вихрей образовалась Земля.
Хотя у теории Левкиппа-Демокрита было немало последователей, но наиболее влиятельные в античности философские направления – Платона и Аристотеля – отвергали их вихревую теорию, и считали лежащими в основе устройства Природы не спиральные- вихревые, а прямолинейные и круговые движения. Впрочем, ближе к концу античного периода вихри-спирали стали применять, в попытках объяснения явлений природы, философы и этих школ. Так Ксенарх (–80/–75 - +10 гг.), последователь Аристотеля, считал спиральное движение фундаментальным, подобно движению по прямой и по окружности, поскольку любая часть спирали совпадает с любой другой частью[4].
Античных инженеров-механиков интересовали более практические применения спиралей, и, прежде всего, винты, устройства, преобразовывавшие вращательные движения в поступательные. Архимед (–287 - –212 гг.) из Сиракуз построил архимедов винт – конструкцию для подъёма воды вверх с помощью винта внутри цилиндра (он же ввёл в математике спираль Архимеда – фигуру, получаемую сочетанием поступательного и вращательного движений). Герон Александрийский (усл. –I в.) написал трактат о винтах, придумал паровую турбину – шар, вращаемый вокруг своей оси силой водяного пара.
Проблемы преобразований движений одного вида в другие, применения винтов привлекали внимание инженеров Итальянского Ренессанса. В оборот вновь вошли сочинения на эту тему математиков и механиков античности, в т.ч. Архимеда и Герона.
Винтами и спиралями интересовался Леонардо да Винчи (1452 - 1519 гг.); их изображения сохранились в его набросках. Он также был автором винтовой лестницы в замке Шамбор; придумал воздушный винт, с помощью которого мог подниматься в воздух летательный аппарат, прообраз вертолёта. (См. далее главу "Спирали в творчестве Леонардо да Винчи").
Ближе к концу эпохи Возрождения вихри-спирали обратили на себя внимание философов и физиков, занятых поисками причинно-следственных объяснений явлений природы.
XVII - XVIII вв.
Французский математик, физик и философ Рене Декарт (1596 - 1650 гг.) считал, что действия одних тел на другие, не имеющие между собой видимого контакта (например. влияние магнита на железо или Луны на приливы) переносятся вихрями в эфире – некоторой среде, заполняющей всё пространство. Эту теорию он изложил в трактате "Начала философии" (1644 г.).
 Вихри Декарта.
Вихри Декарта.
Вихрям Декарт придал главную роль и в своей космогонической гипотезе, которую он изложил в том же трактате. Из начального хаоса, или эфира, благодаря взаимодействиям частиц, образовались первичные вихри. Из них затем возникло Солнце, ставшее центром огромного вихря. Более массивные частицы вытеснялись к периферии, сцеплялись, и из вторичных вихрей возникли планеты. Каждая планета вовлекалась своим вихрем в круговое движение вокруг Солнца. Кометы также образовались из пограничных вихрей материи.
Теория Декарта о передаче воздействий на расстояниями вихрями в эфире, как и, тем более, его космогония, не имели математических моделей или опытных обоснований. Тем не менее, они нашли многочисленных последователей.
Вихревая теория тяготения (последователи Декарта)
Голландский физик Христиан Гюйгенс (1629- 95 гг.) развивал эфирно-вихревую теорию Декарта, ставил опыты для её подтверждения. В своих работах 1660- 70- гг. он дал основанную на представлениях о вихрях в эфире теорию тяготения. Позже, в 1690 г., он изложил её в "Трактате о свете", точнее, в приложенном к нему "Рассуждении о причине тяжести".
Исаак Ньютон (1643 - 1727 гг.) критически отнёсся к идеям Декарта; в частности, он полагал, что эфирно-вихревая теория французского учёного не подходит для объяснения тяготения, законы которого он привёл в своих "Математических началах натуральной философии" (1684- 86 гг.).
Невзирая на критику со стороны Ньютона, в XVII-XVIII вв. последователи Декарта пытались и далее построить теорию тяготения, используя понятие вихрей в эфире; в частности, вывести, с их помощью, законы Кеплера для орбит планет и законы Ньютона. Этим занимались швейцарские математики братья Яков и Иоганн Бернулли, Даниил Бернулли, сын Иоганна; немецкий физик Георг Бильфингер; французский механик и математик Пьер Вариньон и другие. В 1720- 40-х гг. Парижская академия регулярно объявляла годичные конкурсы на построение теорий тяготения в духе гипотезы Декарта (чтобы противопоставить её теории англичанина Ньютона).
В 1728 г. Георг Бильфингер (1693 - 1750 гг.), в то время профессор Санкт-Петербургской академии наук, получил премию Парижской академии за работу по объяснению причин тяготения. Он трактовал тяготение как результирующую центростремительных сил двух вихрей, имевших общий центр в Земле и взаимно перпендикулярных.
Иоганн Бернулли (1667 - 1748 гг.) и Даниил Бернулли (1700- 82 гг.) представляли тяготение как явление, вызванное потоком частиц к центру вихря. В 1730 г. И. Бернулли получил премию Парижской академии за работу, в которой объяснял, с точки зрения декартовой теории вихрей, эллиптические формы орбит планет и изменения положения их больших осей. В 1732 и 1734 гг. И. и Д. Бернулли получил премии Парижской академии за работы по объяснению взаимных наклонов орбит планет.
В 1735- 36 гг. французский астроном Жак Кассини (1677 - 1756 гг.) написал два сочинения о применении гипотезы Декарта для объяснения движений планет.
В 1752 г. французский астроном и популяризатор науки Бернар Фонтенель (1657 - 1757 гг.), член Парижской академии, издал трактат под названием "Теория картезианских вихрей, вместе с размышлениями о тяготении" (Théorie des tourbillons cartésiens; avec des Réflexions sur l'attraction), в которой поддержал взгляды Декарта и попытался показать, что на них можно основать теорию тяготения.

Гипотеза Декарта о вихревом происхождении Вселенной тоже получила некоторое развитие. В 1732 г. шведский философ и теолог Эммануил Сведенборг (1688 - 1772 гг.) изложил в труде ""Принципы природы" космогоническую концепцию, по которой из хаотичной материи возникали плотные сгустки (зародыши звёзд); затем в них, из-за спирального движения частиц, возникали вихри, которые захватывали другие частицы, из которых формировались шары с горячим ядром и темной коркой, вращавшейся вокруг ядра. Постепенно под действием центробежных сил корка истончалась и лопалась; центр шара открывался, образуя звезду, а осколки корки образовывали сначала кольцо вокруг этой звезды, а потом будущие планеты. Идеи Сведенборга повлияли на космогонические гипотезы Канта (1755 г.), Лапласа и др.
В дальнейшем в научном сообществе, включая и французское, возобладали представления о тяготении, развитые Ньютоном, а декартова теория вихрей была надолго оставлена.
XIX в.
Если эфир и, тем более, вихри в нём, были ненаблюдаемыми, представляли собой введённые для объяснения феномена воздействия одних тел на другие гипотетические понятия, то в природе имелись реальные объекты, в которых вихри, спиральные движения были очень даже заметными – жидкости и газы. С середины XVIII века начала развиваться математическая гидродинамика, а внутри неё – теория вихрей в жидкости. Их изучали Эйлер, Коши, Стокс, У. Томсон, Гельмгольц, Кирхгоф и другие.
Швейцарско-российский математик Леонард Эйлер (1707- 83 гг.) связал понятие вихря в жидкости с вращательными движениями малых элементов объёма. В 1816 г. французский физик и математик Огюстен Луи Коши (Cauchy) (1789 - 1857 гг.) дал более строгое определение вихря – как угловой скорости вращения элемента жидкости, а в 1845/7 г. ирландский физик и математик Джордж Стокс (1819 - 1903 гг.) ввёл числовую меру завихрённости поля скоростей u(x, y, z): rot u = (¶u/¶z – ¶u/¶y, ¶u/¶y – ¶u/¶x, ¶u/¶x – ¶u/¶y).
Эйлер также вывел уравнение для безвихревого движения жидкости, и нашёл, что для его поля скоростей u(x, y ,z) должна существовать скалярная функция j (потенциал) такая, что u = Ñj.
Стокс и другие вывели уравнения для вихрей w = rot u у различных видов жидкостей.
В работах Коши (1827 г.), Стокса (1845 г.), Гельмгольца ( 1858 г.) было показано сохранение вихрей/ вихревых колец (в разных терминах) в идеальной жидкости.
Немецкий физик Герман Гельмгольц (1821- 94 гг.) в своём трактате 1858 г. "Об интегралах уравнений гидродинамики, соответствующих вихревым движениям" доказал ряд теорем о вихрях в жидкости, в т.ч.: 1) частицы жидкости, расположенные на некоторой вихревой линии, при своем перемещении всегда будут принадлежать к той же линии; 2) вихревые линии внутри жидкости либо замкнуты, либо оканчиваются на её границе.
* * *
Параллельно с математической гидродинамикой, лишь несколько отставая от неё, развивалась аэродинамика, имевшая с первой много общего в предмете исследования (газы и жидкости близки по своим свойствам). В ней также изучались вихри.
Развитие математической гидродинамики, в т.ч. разработка в ней теории вихрей, оказывали влияние на теории света, магнетизма и электричества, поскольку эти воздействия, по тогдашним представлениям, происходили через посредство эфира, который наглядно представлялся чем-то вроде жидкости с особыми свойствами (в более поздних моделях – аналогом сплошной упругой среды). Электродинамика, как и теория света (эти направления слились вместе только после работ Дж. Максвелла) в XIX в. брала многие свои понятия, представления и методы из гидродинамики, в частности, распространения магнитных и электрических воздействий представлялись аналогами распространения возмущений в жидкости.
В 1850- 60-х гг. шотландские физики Уильям Томсон (Кельвин) (1824 - 1907 гг.) и Джеймс Клерк Максвелл (1831- 79 гг.), занимаясь изучением электричества и магнетизма, пришли к выводу, что магнитные силы имеют вихревой характер. В теории, разрабатывавшейся Максвеллом в 1860- 70-х гг., магнитное воздействие представлялось как вращение одних вихрей (в эфире), а воздействие электричества – как поступательное движение других вихрей. В уравнениях электромагнитного поля, выведенных Максвеллом, динамику электрического поля определял ток электричества и вихрь магнитного поля; и обратно, динамику магнитного поля определял вихрь электрического поля.
Максвелл вывел[5] уравнение для силы F, действующей на заряжённую частицу, движущуюся со скоростью v в электрическом поле E и магнитном поле B:
F = q(E+ [v, B])
Как следствие, отсюда можно вывести, что заряжённая частица в однородном магнитном поле (E = 0, B = const) будет двигаться по спирали (винтовой линии на цилиндре), что многократно и наблюдалось (см. иллюстрации выше).
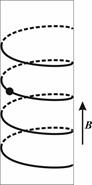 Движение заряжённой частицы в однородном
магнитном поле.
Движение заряжённой частицы в однородном
магнитном поле.
Хотя концепция эфира через некоторое время отошла в физике иа второй план, это по сути не оказало влияния на уравнения Максвелла для электромагнитного поля. Впрочем, эфирную теорию электромагнетизма продолжал развивать в 1-й трети XX в. ряд английских учёных, в т.ч. У. Хикс (1850 - 1934 гг.), Дж. Фитцджеральд (1851 - 1901 гг.), Дж.Дж. Томсон (1856 - 1940 гг.) и другие; также советские физики В.Ф. Миткевич (1872 - 1951 гг.), А.К. Тимирязев (1880 - 1955 гг.), Н.П. Кастерин (1869 - 1947 гг.).
середина XIX - начало XX вв.
Шотландский физик и инженер Уильям Ранкин (Rankine) (1820- 72 гг.), один из основателей классической газовой динамики, в феврале 1850 г. прочитал в Королевском обществе Эдинбурга два доклада, под названиями "О центробежной теории упругости и ей приложении к газам и парам" (On the centrifugal theory of elasticity, as applied to gases and vapours), "О механическом действии тепла, особенно в газах и парах" (On the mechanical action of heat, especially in gases and vapours)[6]. В них Ранкин изложил разработанную им теорию молекулярных вихрей, по которой атомы состоят из ядра в центре и газообразной оболочки вокруг него, частицы которой, с одной стороны, удерживаются около центра вследствие притяжения ядром, а с другой – испытывают центробежные силы из-за своего вращения или осцилляции вокруг него. Из-за такого сочетания сил вся конструкция является упругой, что позволяет дать объяснение явлению распространения тепла. Ранкин также представил во время чтения докладов сделанные им из проволоки модели предположительных структур атомов. Его идеи повлияли на Максвелла и У. Томсона, с которыми Ранкин переписывался[7].
Шотландский физик и инженер Уильям Томсон (Кельвин) (1824 - 1907 гг.) с конца 1860-х гг. разрабатывал вихревую теорию строения материи, в основу которой было положено понятие вихревого атома. Идею последнего он взял из теоремы о сохранении вихревых колец в идеальной жидкости, доказанной в середине XIX в. в рамках гидродинамики. В работе "О вихревых атомах" (1867 г.)[8] он представлял атомы как кольцевые вихри, плавающие в эфире. В качестве наглядной иллюстрации такого подхода Томсон привёл опыт с дымовыми кольцами (продемонстрированный его коллегой Питером Тейтом), когда эти кольца, плавающие в воздухе, упруго отталкивались при столкновениях друг с другом, сохраняя форму – поведение, которого можно было бы ожидать и от атомов.
Такая модель атомов, по мнению Томсона, имела ряд преимуществ перед представлением о них, идущем от античных атомистов (Левкипп-Демокрит, Лукреций Кар) и сохранившимся до Ньютона, в котором "неделимые" считались чем-то вроде материальных точек. Упругость атомов-"колец в эфире" могла дать объяснение распространению тепла, спектрам элементов (Томсон упоминал в связи с этим модель Ранкина) и другим наблюдаемым в природе явлениям, для чего модель "жёстких" атомов Лукреция-Ньютона была, как он считал, почти непригодна.
Представления об эфире также подверглись им переработке. В 1880 г. У. Томсон ввёл модель эфира, как аналога идеальной несжимаемой жидкости, заполненной мелкими вихрями- вихревую губку. (Сходную модель эфира- вихревой губки рассматривал ещё в 1736 г. И. Бернулли, пытаясь с её помощью объяснить эффекты распространения света). В 1880-х гг. Томсон написал ряд работ по вихрям в эфире; продолжая модифицировать структуру эфира.
Теория "вихревых атомов" приобрела популярность среди английских физиков: в 1870- 90 гг. на эту тему около 25 учёных написали порядка 60 работ. Темы, связанные с вихревыми губками и вихревыми кольцами, включая проблемы их устойчивости, распространения в них возмущений и пр. разрабатывали У. Хикс, Дж. Фитцджеральд, Дж.Дж. Томсон и другие.
Джозеф Джон Томсон (1856 - 1940 гг.), первооткрыватель электрона (1897 г.), в ряде статей и книг 1880 - 1920-х гг. ("О движении вихревых колец", "Электричество и материя", "Структура света"[9] и др.) развивал вихревую теорию материи.
 "О движении вихревых колец"
"О движении вихревых колец"
С её помощью он давал объяснения различным физическим явлениям: электрическим разрядам в газах, распространению тяготения, спектрам излучений, квантованию энергии, связи массы и энергии[10] и т.д.
В статье 1924/5 г. "Структура света" Томсон представил квант света в виде тороидальной фарадеевской силовой трубки. Она двигалась перпендикулярно своей плоскости, "неизменно по величине и форме", не теряя энергии во время движения. Поглощение материей света приводило к "размыканию" таких квантовых колец.

Сходное строение имели кванты излучений и других типов, в т.ч. рентгеновского.
Эти кольца- фотоны окружало, во время их движения, переменное электромагнитное поле, так что они как бы сочетали в себе корпускулярную (соотносимую с самим фотоном) и волновую (соотносимую с сопровождающим его полем) структуры.
Используя свою модель, Томсон дал объяснения явлениям дифракции, интерференции света; привёл доказательство закона Планка о связи энергии и частоты и вывод постоянной Планка[11].
Биология
Филлотаксис (основные термины, факты, модели)
ботанические термины и факты; биохимические термины и факты;
ботанико-математические термины и факты
Филлотаксисом называется расположение (греч. taxis) листьев (греч. phylla) или их аналогов (цветков, колючек, чешуек шишек и пр.) на растениях.
Филлотаксис издавна интересовал ботаников, математиков, других учёных – и как средство для классификации растений, и в связи с вопросами построения его математических моделей, и при изучении причин рост растений.
Нетрудно заметить, что в расположении листьев (цветков, семечек подсолнуха, чешуек сосны и т.д.) часто выделяются два семейства спиралей, одни лево-, другие правозакрученные. При этом количества таких спиралей- парастихов (греч. боковые ряды) в семействах обычно составляли пары последовательных чисел из ряда Фибоначчи.

Схематическое изображение филлотаксиса[12].
Далее, можно заметить, что угол между последовательно появляющимися листьями (цветками, …) и центром растения в большинстве случаев был постоянным, и также связанным с радом Фибоначчи – он определялся числом спиралей- парастихов.
В связи с этими фактами, отмеченными уже в XIX веке, возник ряд вопросов:
1) Почему листья растут по спиралям, притом близким к логарифмическим?
2) Почему в большинстве случаев числа парастихов – пары из ряда Фибоначии?
3) Почему угол расхождения между последовательно появляющимися листьями постоянен, и притом определяется числом парастихов (и т.о. рядом Фибоначчи)?
Термины, факты и модели, используемые при изучении филлотаксиса, можно разбить на три класса: общие ботанические, специальные биохимические, и математические.
*) Стебель; боковые вегетативные органы (листья, …).
*) Меристема (греч. μεριστός - делимый) – группа интенсивно делящихся клеток, из которых образуются различные специализированные ткани растения.
*) Апекс – верхушка побега, в которой расположен конус нарастания. Побег верхушечной меристемы (shoot apical meristem, SAM). Центральная зона (ЦЗ) SAM.
*) Примордий – нерасчленённый зачаток листа и других боковых органов растения (почек, частей цветка, лепестков, тычинок, … ); в виде бугорка или валика на конусе нарастания побега, состоящий из однородных меристемных клеток. Начальная стадия формирования боковых органов, в которые они превращаются в процессе роста и удаления от центра растения. После появления примордии движутся от центра, освобождая место для следующих.
*) Правило Хофмейстера. Примордии появляются на краю центральной зоны (ЦЗ) апекса, притом на месте, наиболее свободном/ наиболее удалённом от других примордий.
*) Ауксин – гормон роста в растениях; низкомолекулярное вещество, производное триптофана
Градиенты ауксина в тканях определяют процессы деления, роста и дифференцировки клеток.
В первые дни после прорастания ауксин синтезируется только в апексе побега, в примордиях и молодых листьях; затем синтез может происходить в разных частях растения; однако основным постоянным источником ауксина в растении является апекс побега.
В биохимических моделях морфогенеза распределение ауксина является ключевым фактором.
Ботанико-математические термины и факты
Пусть некоторая основная часть растения спроектирована на плоскость, перпендикулярную стеблю. Далее рассматривается эта проекция. Пусть Pn – последовательность центров примордий и боковых органов, упорядоченная по времени появления, начинающаяся с меристемы. Проекцию самой меристемы можно представить в виде круга,
*) Примордии и образовавшиеся из них органы расположены на генетической спирали. Она близка к логарифмической спирали.
*) Последовательные элементы примордий и боковых органов (Pn) образуют равные углы с центром O генетической спирали, на которой они лежат; Pn+1OPn = a = const. Он называется угол расхождения.
*) Примордии и боковые органы образуют два семейства контактных (видимых) парастихов (греч. парные ряды), также близких по форме к логарифмическим спиралям; одни из них лево-, другие правозакрученные.
(m, n) - пара чисел- количества спиралей в семействах левых и правых парастихов называется модой филлотаксиса; при этом m и n являются парой последовательных чисел из ряда Фибоначчи в большинстве случаев, называемых регулярными; или из ряда Люка для большинства остальных.
У цветов обычны моды (3, 5) или (5, 8), хотя у маргариток она (21, 34); у сосновых шишек обычны моды (5, 8) и (8, 13); у подсолнечника – (34, 55), но бывают и (55, 89), и даже (89, 144).
Правило Брауна: если к элементу Pk с номером k на генетической спирали примыкают сверху (слева и справа) элементы с номерами k+m и k+n, то мода филлотаксиса будет (m, n).
Мода филлотаксиса, т.е. числа спиралей- парастихов определяет величину угла расхождения, а именно, если мода = (pn, pn+1), где pi из ряда Фибоначчи, то угол расхождения a = (pn-1/pn+1)*360°, что близко к 137°. Дроби pn-1/pn+1 представляют собой приближения непрерывной дроби [2, 1, 1, …], значение которой равно 1/t2, где t - золотое сечение (» 1,1618). Угол расхождения (1/t2) *360° называется золотым углом (»137°30').
Если мода = (ln, ln+1) где li из ряда Люка (таково большинство нерегулярных случаев), то угол расхождения = (pn-1/ln+1)*360°, что близко к 99,5°. Эти дроби представляют собой приближения непрерывной дроби [3, 1, 1, …],
*) Ортостихи – вертикальные линии, образуемые боковыми органами.
 Ортостихи у кактуса.
Ортостихи у кактуса.
Они характеризуются парой целых чисел (p, q), или, в других обозначениях, дробью p/q; где p – число витков на генетической спирали от одного элемента до его вертикального соседа, q – число элементов в этих витках (т.е. от одного элемента до расположенному над ним).
Как правило, они не вполне вертикальны, а представляют собой близкие к прямым спирали,
Для вяза и липы дробь ортостихи обычно 1/2, для ольхи – 1/3, для вишни, сливы, дуба – 2/5.
Лучше всего вертикальные ряды (ортостихи) видны у многих видов кактусов.
Если у растения есть ортостихи порядка p/q, то угол расхождения его генетической спирали = (p/q)*360о.
*) Примордии появляются на границе региона апекса; через равные промежутки времени. Платохрон T – время между появлениями последовательных примордий.
*) Пластохронное или радиальное отношение = rn+1/rn, где ri – расстояние примордия или бокового органа Pi до центра спирали O. Поскольку примордии и образовавшиеся из них органы расположены на почти логарифмической спирали и притом на равных углах от центра (см. пункт выше), то радиальное отношение является почти константой.
*) Примордии расходятся от центра растения относительно равномерно.
Радиальная скорость V – скорость расхождения примордий от центра растения.
VT – сколько пройдёт в радинальном отношении примордий за один пластохрон; расстояние (по радиусу, т.е. rn+1 – rn), которое образуется между примордиями за один платстохрон.
*) Примордии и образованные из них боковые органы увеличиваются в размерах с течением времени.
*) Радиус центральной зоны апекса R. Может медленно меняться со временем.
Для подсолнечника R уменьшается; для сосновых шишек и кактуса увеличивается.
*) Индекс роста G = VT/R. Это отношение радиального расстояния между примордиями, т.е. (rn+1 – rn), к радиусу центральной зоны.
Если режим появления (промежутки и времени и скорость) примордий не меняется, а радиус центральной зоны увеличивается (что обычно бывает с возрастом у растений), то индекс роста падает.
*) Кусочно-регулярный филлотаксис –параметры (m, n) (мода), a (угол расхождения), T (пластохрон), V (скорость появления новых примордий), R (радиус центральной зоны апекса) примерно постоянны на некоторых промежутках времени (ti, ti+1). При этом числа спиралей- парастихов (m, n) – из ряда Фибоначчи.
*) (Возможное) изменение моды филлотаксиса (m, n) на (m', n') при переходе от участка (ti, ti+1) к участку (ti+1, ti+2) называется переходом порядка. Основные переходы порядка: (m, n) -> (m+n, n) или (m, m+n); также обратные. Переход порядка зависит от индекса роста, главным образом от изменения радиуса ЦЗ апекса. Диаграмма Итерсона иллюстрирует эти возможные переходы мод филлотаксиса и показывает связь между индексом роста и модой (а, значит, и углом расхождения).
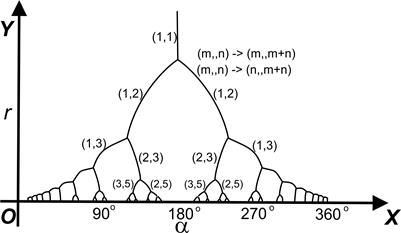
решётки Браве; представление Итерсона; представление Чёрча
численное (компьютерное) моделирование
физическое моделирование; механистические модели
биохимические теории; теории поля; теории самоорганизации
Решёткой Браве называется отображение примордий и боковых побегов Pi (расположенных на генетической спирали) в точки на полосе плоскости (или на цилиндре), с координатами (xi, yi) так, что xi = xi-1 + a (mod 2p), yi = yi-1 + ln(rn/ri-1).
Точки будут лежать в полосе [0, 2p) * [0, µ); образовывать ромбическую либо гексагональную решётку.
Поскольку спираль, на которой расположены Pi, является (почти) логарифмической, то rn/ri-1 будет (почти) постоянным, а, значит, (yi - yi-1), задающие расстояние между точками решётки по оси OY, будут (почти) постоянными.
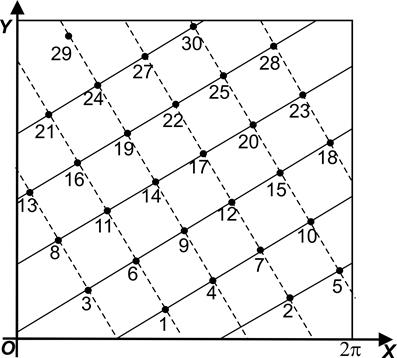
Генетическая спираль, как и оба семейства парастихов, изобразятся на решётке Браве в виде параллельных между собой отрезков прямых. Коэффициент их наклона определяется параметром соответствующих спиралей. При этом лево- и правозакрученные парастихи отобразятся в отрезки прямых с коэффициентами наклона разных знаков.
Отображение является конформным, поэтому оно сохраняет углы между парастихами (т.е. углы между касательными к парастихам будут равны углами между их образами- отрезками).
Отображение примордий и боковых побегов Pi в круги равного диаметра с координатами их центров в точках (xi, yi) решётки Браве, притом такое, чтобы их упаковка была наиболее плотной и без перекрытия (т.е. чтобы они по возможности соприкасались друг с другом).
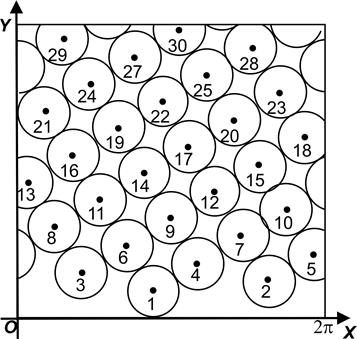
На представлении Итерсона удобно иллюстрировать правила, или диаграмму Итерсона (см. выше). А именно, если размер дисков уменьшается (что происходит, напр. при увеличении радиуса апекса, т.е. при падении индекса роста), то их расположение меняется, напр. диск №9 приближается к диску №1, оттесняя №4, и т.о. через некоторое время он станет соседним с диском №1, и, значит, имеющаяся здесь мода (3, 5) перейдёт в моду (5, 8), по правилу (m, n) -> (n, m+n). Если же №9, приближаясь к диску №1, оттеснит №6 (а не №4),, то исходная мода (3, 5) перейдёт в моду (3, 8) (не фибоначчиеву).
Нетрудно видеть, что промежуточным между модами (3, 5) и (5, 8)/ (3, 8) некоторое время будет гексагональное расположение с тремя контактными парастихами, а именно, когда диск №1 будет касаться одновременно №6, №9 и №4. На диаграмме ван Итерсона такому филлотаксису соответствуют точки ветвления.
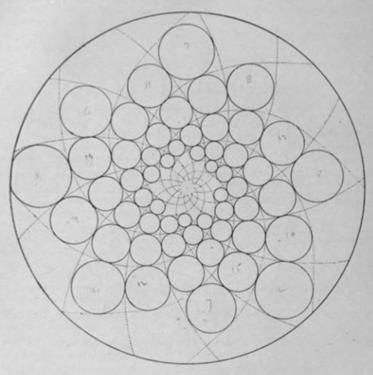
Отображение примордий и боковых побегов Pi в круги, касающиеся сторон криволинейных четырёхугольников, образуемых пересечениями парастихов[13].
Численное (компьютерное) моделирование
Задавая основные параметры филлотаксиса – а именно, угол расходения (a), пластохрон (T) и радиальное отношение (rn+1/rn), а также радиус центральной зоны (R; в простейшихт случаях его можно положить = 0) можно строить точки на логарифмической спирали, соответствующие этому филлотаксису – его численные и геометрические модели.

Филлотаксис 2/5, с пластохронным отношением 1,2 и таким же ростом радиусов. Заметны ортостихи.
Если p/q – некоторая дробь, приближающая угол расхождения a, то филлотаксис с a будет близко к филлотаксису с (p/q)*360о, только ветви будут искривляться; ортостихи будут менее заметными.
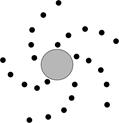
Филлотаксис 41/100 (= 2/5 + 0,01). Ортостихи искривились.
Разлагая a в цепную дробь и строя филлотаксис с соответствующими (pi/qi) можно получать всё более точные приближения для филлотаксиса с углом a.
Проблемы, касающиеся филлотаксиса, можно изучать на физических моделях того или иного , типа, имитирующих процессы появления в апексе примордий, их дальнейшего расхождения и роста. Так, в эксперименте французских физиков Стефана Дуади (Douady) и Ива Кудера (Couder) однородные капли ферромагнитной жидкости (аналог примордий) периодически капали в центр круглого, наполненного нефтью блюда (аналог апекса). На них оказывало воздействие вертикальное магнитное поле, возрастающее к краям от центра, в результате чего они двигались от центра. Также они взаимно отталкивались (дипольным взамодействием), поэтому каждая стремилась в наиболее удалённое от других место (в соответствии с правилом Хофмейстера для примордий). В результате, при некоторой вариации времени между падениями капель (аналога пластохрона) и величины магнитного поля, частицы, попавшие в нефть, двигались по спиралям, при этом угол расхождения между ними оставался постоянным. Вариациями параметров можно было также добиться приближения угла расхождения к золотому углу (2p/t2), характерному для регулярного филлотаксиса, и появления спиралей парастихов с модой из чисел Фибоначчи.
В них формирование филлотаксиса рассматривается как задача оптимальной упаковки дисков (или других фигур) при некотором росте всей системы. Смена моды филлотаксиса (переход порядка) происходит в результате перестройки системы парастихов при изменении характера оптимальной упаковки, что иллюстрируется диаграммой ван Итерсона (см. выше).
В теориях такого типа изучаются уравнения, определяющие распределение (скалярное поле) в апексе ауксина (гормона роста) и ингииторного воздействия примордий на другие. Динамика поля ауксина u(x, y, t) определяется в некотором приближении уравнением типа Свифта-Хоненберга:
u t = −(∇2 + 1)2u + μu − β∇(u∇u) − u3
К ним можно отнести все теории, в которых динамика системы (в данном случае – появления и роста примордий) определяется экстремумом некоторого функционала – характеризуемого как действие, либо как энергия и пр., что эквивалентно решению некоторых уравнений поля, как и в обычных физико-математических моделях. Сюда включаются и биохимические модели, и задачи наиболее плотной упаковки дисков.
Попытки объяснения филлотаксиса через поведение нестабильных динамических систем. Рассматриваются скалярные поля гормона роста (ауксина) и напряжений (или давлений) в регионе SAM. Далее изучаются аттракторы, или устойчивые состояния этих систем.
Изучение спиральных структур в биологии (исторический обзор)
Кеплер, Сваммердаам, Бонне
Шимпер-Браун; Хэнслоу-ст.; Браве
изменение порядка филлотаксиса
Античность
Спиралевидные структуры, часто встречающиеся в живой природе (см. выше иллюстрации), несомненно, были замечены уже в древности, и скорее всего, именно они оказали влияние на создателей изображений спиралей в произведениях искусства и архитектуры цивилизаций Малой Азии, Ближнего Востока, Средиземноморья. Возможно, они привлекли к себе внимание также и ранних натурфилософов[14].
В античной Греции Теофраст (–370 - –285 гг.), ученик Аристотеля и автор сочинений по ботанике отметил правильность расположения листьев на растениях. Он писал, что "у деревьев с плоскими листьями листья расположены правильными рядами, как, например, у мирта"[15]. Позже Плиний Старший (22/24 - 79 гг.) в своей "Естественной истории" сказал об этом чуть подробнее, а именно, при описании апарина[16], он сообщил, что листья этого растения располагаются по 5 или 6 на одной ветке, с регулярными интервалами[17].
Однако спирали в расположении листьев растений, насколько можно судить по дошедшим текстам, в античных теоретических работах по ботанике описаны не были.
Впрочем, спирали привлекли к себе в то время внимание математиков, инженеров-механиков и философов (см. выше).
Возрождение
Начиная с эпохи Возрождения, в Европе вновь стали популярными пифагорейско-платонические представления об устройстве Природы по математическим образцам, что повлекло за собой рост интереса к познанию числовых закономерностей и геометрических форм как в физике, так и в мире растений и животных.
На математические закономерности в расположении листьев обратил внимание Леонардо да Винчи (1452 - 1519 гг.), отметивший в одной из своих записных книжек, что листья в процессе роста на раннем этапе поворачиваются и располагаются на ветке так, что первый лист оказывается над шестым[18]. Его наблюдения были связаны с начавшейся тогда математизацией знания. Сам Леонардо да Винчи писал "Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой".
Итальянский медик и натурфилософ Андреа Чезальпино (1519 - 1603 гг.) в своём сочинении 1583 г. "16 книг о растениях" (De plantis libri XVI), посвященном систематике цветочной флоры, наиболее важное значение придавал формам растений и количественному анализу их частей[19]. Он отметил регулярность в расположении их листьев.
Сама математика с XV - XVI вв. тоже стала быстро развиваться, во многом под воздействием возрождения в это время пифагорейско-платонических идей. В частности, в ней появилось описание логарифмической спирали – сначала, в нестрогой форме, в книге 1525 г. "Рассуждения об измерениях циркулем и линейкой" (Unterweisung der Messung mit dem Zirkel und Richtscheit) немецкого художника и математика Альбрехта. Дюрера (1471 - 1528 гг.), потом, у Рене Декарта (1596 - 1650 гг.), давшего определение равноугольной кривой. В математике эпохи Возрождения стало также изучаться золотое сечение (которое, как несколько позже выяснилось, имело прямое отношение к геометрии объектов живой (и неживой) природы). Профессор математики ряда итальянских университетов Лука Пачиоли (1447 - 1517 гг.) написал книгу о свойствах золотого сечения, а Леонардо да Винчи нарисовал к ней иллюстрации. В книге рассматривались чисто математические свойства золотого сечения.
Немецкий астроном Иоганн Кеплер (1571 - 1630 гг.) полностью поддержал представление, что Природа устроена по математическим образцам: "Следы геометрии запечатлены в мире так, словно геометрия была прообразом мира". Сам он не только ввёл ряд математических законов в астрономии, но и обратил внимание на геометрические формы в живой природе, в частности, на расположение лепестков цветов в форме правильных пятиугольников, а также отметил, хотя и в несколько неясных выражениях, возможную связь роста растений с числами из ряда Фибоначчи. В работе 1611 г. "О шестиугольных снежинках (De nive sexangula) он писал: "Если спросят, почему у всех деревьев и кустарников или, по крайней мере, у большинства из них цветы, распускаясь, приобретают пятиугольную форму, то есть имеют по пяти лепестков,… то я отвечу, что здесь рассуждения о красоте и свойствах фигуры, в которых проявляется душа растения, были бы вполне уместны. … Построение … пятиугольника невозможно без той пропорции, которую современные математики называют божественной[20]. (далее в тексте описан ряд Фибоначчи) … По образцу и подобию этой продолжающей себя пропорции сотворена, как я полагаю, производительная сила, и этой производительной силой запечатлен в цветке подлинный смысл пятиугольной фигуры"[21]. Эти рассуждения были приведены Кеплером в контексте общего рассмотрения им геометрических форм в живой природе – включая формы пчелиных сот, зерен граната и пр.
Примерно в то же время натуралисты обратили внимание на спиралевидные формы раковин моллюсков. Голландский медик, анатом, энтомолог Ян Сваммердаам (1637- 80 гг.) в своей книге "Библия природы" (Biblia naturæ) отметил, что раковины моллюсков родов Helix и и Spirula имеют геометрически сходный общий тип[22].
Швейцарский натуралист, медик и философ Шарль Бонне (1720- 93 гг.) в работе 1754 г. "Исследования по расположению листьев в растениях" (Recherches sur l'usage des feuilles dans les plantes) отметил, что листья растений в последовательном появлении один над другим образуют спираль (генетическую), и что, соединяя пространственно близкие листья можно получать ещё одну спираль. На последнее обстоятельство его внимание обратил швейцарский математик и ботаник Жан-Луи Каландрини (1703- 58 гг.). Бонне ввёл термин филлотаксис (греч. расположение листьев).
Бонне дал телеологическое объяснение спиралевидному расположению листьев: при нём листья минимально перекрывают один другого, что обеспечивает растению в целом наилучший доступ воздуха.
С первой четверти XIX века внимание натуралистов, физиков и математиков всё чаще стали привлекать спиралевидные формы раковин моллюсков.
Немецкий палеонтолог, картограф и писатель Иоганн Рейнеке (Reinecke) (1770 - 1818 гг.) в работе 1818 г. об аммонитах Maris protogaei Nautilos высказал предположение, что отношение значений ширины соседних завитков у этих моллюсков имеет определённый и постоянный характер (по существу, это эквивалентно утверждению, что формы раковин представляют собой логарифмические спирали). Эту идею поддержал немецкий геолог Леопольд фон Бух (1774 - 1853 гг.)[23].
Шотландский физик и математик Джон Лесли (Leslie) (1766 - 1832 гг.), рассматривая в своём трактате 1821 г. "Геометрический анализ и геометрия кривых" (Geometrical Analysis and Geometry of Curve Lines) логарифмическую спираль, писал, что она "в точности походит на элегантные формы (раковин моллюска) Nautilus"[24]
Изучение порядка расположения листьев у растений, начатое Ш. Бонне, было продолжено в 1-ой половине 1830-х гг. в работах немецких ботаников Карла Шимпера (1808- 80 гг.) "Описание symphytum zeyheri и двух его немецких родственников …"[25] и Александра Брауна (1805- 77 гг.) "Исследование расположения чешуек на сосновых шишках" [26]. Они отметили, что листья растений и чешуйки сосновых шишек, взятые в порядке их появления, располагаются на спиралях, притом углы, которые два последовательных элемента образуют с центром растения имеют постоянное для данного вида значение (угол расхождения). Далее, они заметили, что элементы этих спиралей после некоторого числа оборотов располагаются над прежними, образуя (почти) вертикальные линии (ортостихи (греч. прямые ряды)). Число элементов (листьев, чешуек, …) в каждом таком оборота было одинаковым – это соответствовало постоянству угла расхождения. Таким образом, генетическую спираль характеризовали два числа – количество раз, сколько она оборачивалась вокруг ствола в подъёме от любого листа к тому, что располагался над ним (p), и суммарное количество листьев на этих витках (q). Из таких данных можно было найти угол расхождения. Именно, если над элементом LN с порядковым номером N после p витков окажется элемент с номером N+q, то угол расхождения будет равен (p/q)*360о.
Шимпер и Браун обратили внимание на дополнительные спирали в строении растения, как и Бонне с Каландрини ранее. Соединяя элементы спирали с касающимися их слева, получались левозакрученные спирали, соединяя их с касающимися справа – правозакрученная. Шимпер ввёл для этих спиралей термин парастихи (греч. парные ряды). Браун отметил, что числа парастихов можно установить, рассматривая, какие элементы (пронумерованные в порядке их появления, т.е. на генетической спирали) примыкают сверху к данному. Так, если к элементу N примыкают сверху элементы с номерами N +13 (слева) и N + 8 (справа),то у растения есть 13 левозакрученных и 8 правозакрученных парастихов. Число парастихов получило название порядок филлтаксиса. (В данном случае это была пара (8, 13)). Так как для филлотаксиса порядка (fn-1, fn) угол расхождения составлял (fn-2/fn)*360о, то порядком филлотаксиса можно было называть и дробь fn-2/fn.
Наконец, они обнаружили связь филлотаксиса с рядом Фибоначчи. Во-первых, числа лево- и правозакрученных боковых спиралей обычно составляли пару последовательных чисел из ряда Фибоначчи: (2, 3), (3, 5), (5, 8), (8, 13), … . Во-вторых, пары (p, q) характеризующие генетические спирали (и углы расхождения) также составляли пары чисел из ряда Фибоначчи: (1, 2), (1, 3), (2,5), (3, 8),, только уже не последовательных, а взятых через одного. Вероятно, связь филлотаксиса с числами из ряда Фибоначчи впервые была установлена именно в их работах.
* * *
Результаты Шимпера п Брауна быстро вошли в научный оборот. Английский минералог и ботаник Джон Стивенс Хэнслоу (1796 - 1861 гг.), или Хэнслоу-старший, с 1823 г. профессор Кембриджа, в своём учебнике 1835 г. "Принципы описательной и физиологической ботаники" (The Principles of Descriptive and Physiological Botany), уже изложил основную их часть, хотя и с небольшими ошибками[27].
Независимо от Шимпера и Брауна, но чуть позже их братья Луи Браве (1801- 43 гг.) и Огюст Браве (1811- 63 гг.) в работе 1837 г. "Опыты о спиральном расположении листьев"[28] сделали аналогичные наблюдения и заключения.

Браве в своих исследованиях расположения листьев у растений пошли дальше, чем Шимпер и Браун. Они напрямую связали филлотаксис с золотым сечением (далее обозначается t), которое является пределом отношения последовательных чисел ряда Фибоначчи, и которое может быть представлено в виде бесконечной цепной дроби с единицами. (Числа Фибоначчи получаются при вычислении конечных сумм этой цепной дроби).

Браве не согласились с Шимпером и Брауном в том, что угол расхождения в генетических спиралях должен быт рациональной частью от 360о. (определяемой парой (p, q); см. выше). Построив таблицу значений угла расхождения для возрастающих пар (p, q), они заметили, что эти величины сходятся к jt = 360о*(1/t2) = 360о*(1/(1 + t)) » 137°30'28''. Т.о. чем больше были значения (p, q) = (fn-2, fn) генетической спирали, тем ближе был угол расхождения к jt; который можно было бы назвать идеальным углом расхождения, или золотым углом.
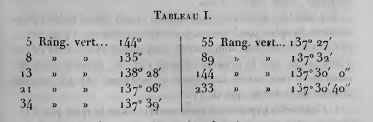
Браве отметили, что у растений встречаются, хотя и редко, и другие расположения листьев, для которых числа парастихов не принадлежат ряду Фибоначчи. В частности, могут быть спирали, с числом парастихов из ряда Люка (1, 3, 4, 7, 11,…); ряда (1, 4, 5, 9, 13,….). Эти ряды получаются аналогично ряду Фибоначчи (суммированием последовательных элементов), только исходя из других первых пар. Соответственно, углы расхождения генетических спиралей у таких растений уже не будут (fn-2, fn), где fn - n-й член ряда Фибоначчи. Для ряда Люка они будут (fn-1, ln), где f обозначает числа из ряда Фибоначчи, а l – из ряда Люка. Углы расхождения в таких случаях будут иметь значения (1/3, 1/4, 2/7, 3/11, …)*360о; числитель дроби получается суммой двух предыдущих числителей, а знаменатель – суммой предыдущих знаменателей. Они сходятся к » 99°30'. Для второй последовательности предел будет » 77°57'.
Браве также представили расположение листьев (или других частей растений) в виде сетки на цилиндре (в развёртке – на плоскости; см. рис. ниже[29]). По существу, это было отображением плоскости, в которой лежат части растений/ их проекции, в себя по зправилу (j, r) -> (j (mod 2p), ln r). При этом отображении вся плоскость переходила в полосу [0, 2p)*[0, µ), а спирали с центром в начале координат переходили в параллельные отрезки прямых, располагавшиеся внутри этой полосы. Соответственно, генетическая спираль и спирали семейств парастихов отображались на три семейства параллельных между собой отрезков, а лежащие на генетической спирали точки (листья, …) – на некоторую решётку. Расстояние по горизонтали между точками этой решётки равнялось величине угла расхождения, а по вертикали – логарифму от отношения расстояний до центра спирали для любой пары последовательных точек (согласно свойствам л.с. оно постоянно).

* * *
Примерно в то же время натуралисты стали отмечать аналогии между расположением листьев у растений и структурой кристаллов. Во-первых, их числовые характеристики и геометрические формы можно было бы использовать для классификации объектов, соответственно, в ботанике и в кристаллографии, Кембриджский профессор Дж Хэнслоу-ст, ботаник и минералог, писал в работе 1836 г. "…[ботаника сейчас] находится во многом в положении, сходном с тем, которое занимала минералогия до открытия законов кристаллографии: минералоги часто сомневались в том, к каким видам следует причислять те или иные кристаллы, и они почти ничего не знали о том, какие формы может иметь данный вид. … Но теперь минералог сразу причисляет конкретный кристалл к некоторому простому виду, и отсюда может априорно сделать выводы о его формах"[30].
Во вторых, симметрия в расположении листьев растений напоминала симметрию структуры кристаллов. Это обстоятельство стало особенно заметным после введения в статье 1837 г. Л. и О. Браве отображения спирального филлотаксиса на плоскую (или цилиндрическую) решётку. Огюст Браве в статьях 1849- 50 гг.[31] ввёл решётки Браве для кристаллов и перечислил их возможные типы. Очевидно, что в этой своей работе по кристаллографии Огюст Браве вдохновлялся идеями его статьи 1837 г. (совместной с братом-ботаником) по филлотаксису.
Продолжались и исследования форм моллюсков. Возник естественный вопрос: какого рода спиралями являются их раковины? Действительно ли они представляют ли они собой уже хорошо изученные к тому времени логарифмические спирали, или они ближе по форме к спиралям Архимеда, или каким-то ещё? Это можно было бы выяснить, проведя аккуратные измерения и используя известные характерные свойства спиралей. Например, если бы оказалось, что при равных приращениях углов завитков раковин их радиус-векторы увеличиваются в геометрической прогрессии, то можно было утверждать, что перед нами логарифмическая спираль.
Такую работу проделал английский математик, механик, натуралист и священник Генри Мосли (Moseley) (1801- 72 гг.).

В своей статье 1837 г."О геометрических формах конусообразных и дискоидных раковин"[32] он показал, что раковины моллюсков Nautilus образуют логарифмические спирали, а потом обобщил это утверждение для аммонитов и моллюсков класса Gastropod (брюхоногие, улитки). Измерив для взятого им образца Nautilus расстояние вдоль радиус вектора от одной точки завитка раковины до точки на следующем завитке вдоль того же направления (т.е. когда угол поворота увеличился на 2p), он обнаружил, что между ними имеет место соотношение 3:1, т.е. длины радиус-векторов при повороте на 2p увеличивались в 3 раза, образуя геометрическую прогрессию. Это означало, что кривая представляет собой логарифмическую спираль[33]. Затем он взял образец моллюска Turbo duplicatus (брюхоногий моллюск); их раковины имели форму спиралей, накручивавшихся на конус[34]. Для соответствующих длин радиус-векторов Мосли получил также (приблизительно) геометрическую прогрессию, с коэффициентом 1,1804:
|
Расстояние до вершины последовательных витков, с конца (в дюймах) |
Геометрическая прогрессия с коэффициентом 1,1804 |
|
1,31 |
1,31 |
|
1,12 |
1,11 |
|
0,94 |
0,94 |
|
0,80 |
0,796 |
|
0,67 |
0,674 |
|
0,57 |
0,57 |
|
0,48 |
0,48 |
|
0,41 |
0,406 |
Поскольку полученный ряд чисел образовывал (почти) геометрическую прогрессию, то это снова была (почти) логарифмическая спираль.
Мосли обнаружил, что разные виды моллюсков характеризуются разными коэффициентами соответствующих геометрических прогрессий, и нашёл их для некоторых Turbo (конусообразных): Turho phasianus имел коэффициент 1,75, Buccinum subulatum – 1,13. Этот коэффициент выражался через угол наклона касательной к логарифмической спирали (который для всех точек кривой был одинаков, согласно одному из характерных свойств л.с.). Так, для Nautilus в вышеприведённом примере (с коэффициентом 3) этот угол составлял около 80о. Он мог быть использован для классификации моллюсков – в частности, углы спиралей раковин у классов моллюсков- обитателей суши и водных моллюсков были различны между собой[35].
Способность моллюсков строить свои раковины в форме почти правильной логарифмической спирали Мосли характеризовал так: "Бог даровал этому скромному архитектору практические умения учёного геометра". Более научно, хотя и не слишком определённо, он объяснял постройку моллюсками раковин в форме (повторяющей себя) спирали "инстинктом строгой универсальности операций" и "принципом экономии"[36].
* * *
После Мосли такие же вычисления для раковин разных видов моллюсков провели немецкий минералог и геолог Карл Фридрих Науман (Naumann) (1797 - 1873 гг.)[37] и другие учёные. Были найдены характеристические коэффициенты геометрических прогрессий для радиус-векторов, и, соответственно, характеристические углы касательных к спиралям раковин.
* * *
С середины XIX века участились попытки дать объяснение феномену роста многих живых организмов – растений, моллюсков – по логарифмическим спиралям. Эти объяснения делились на два типа – телеологические и причинно-следственные. К первым относились попытки представить расположение листьев растений по спиралям с определённым углом расхождения как следствие требования достижения растением максимальной освещённости листьев. Ко вторым – физические и биохимические модели филлотаксиса.
* * *
Шотландский анатом, один из авторов клеточной теории Джон Гудсир (Goodsir) (1814- 67 гг.) в своих лекциях 1849 г. (вошедших в его Anatomical Memoirs, изданный в 1869 г. в Эдинбурге) привлёк внимание к работе Мосли, и подчеркнул важность применения при изучении живых организмов методов математики. Он поставил вопрос: нельзя ли из наблюдаемых нами форм организмов вывести закон их роста, подобно тому, как Ньютон из наблюдаемых форм планетных орбит (эллипсов) вывел закон движения (под влиянием тяготения) физических тел? Отметив высказанное Ньютоном в "Началах" утверждение, что если бы тела притягивались по закону обратных кубов, то они двигались бы по спиралям, Гудсир предположил, что, поскольку наблюдаемый нами рост живых организмов происходит по логарифмическим спиралям то, значит, им управляет (на уровне клетки) закон обратных кубов[38]. Для роста живых организмов он является аналогом закона движения физических тел под влиянием тяготения[39].
Немецкий ботаник, профессор университетов Тюбингена и Гейдельберга Вильгельм Хофмейстр (Hofmeister) (1824- 77 гг.) в своей работе 1868 г. "Общая морфология роста" (в книге "Руководстве по физиологической ботанике"; Allgemeine Morphologie der Gewächse, Handbuch der physiologischen Botanik) дал обзор работ Браве и других, а также изложил собственные взгляды на филлотаксис. В отличие от прежних исследователей, рассматривавших, в основном, зрелые формы растений, он сосредоточил внимание на ранней стадии морфогенеза и появлении примордий в порождающем конусе апекса. Самый важный из сделанных им выводов: новый примордий образуется периодически в пограничном регионе апекса и в наибольшем удалении от предыдущих примордий. Поскольку при задании некоторого закона движения- роста возникших примордий эти правила Хофмейстера почти однозначно определяли динамику морфогенеза, а, значит, и филлотаксис растения, то они стали, вплоть до нынешнего времени, основой большинства физических, математических теорий и численных моделей филлотаксиса, в т.ч. попыток объяснения встречающихся в природе конкретных значений угла расхождения и пр.
В несколько более развёрнутом виде правила Хофмейстера формулировались так:
1. Меристема аксиально симметрична.
2. Примордии почти круглы и они формируются на генеративном граничном кольце апекса.
3. Примордии формируются через постоянные промежутки времени (позже его величина была названа пластохроном).
4, Примордии удаляются от центра апекса с некоторой радиальной скоростью, зависящей от расстояния до этого центра.
5. Каждый новый примордий формируется в месте, наиболее удалённом от остальных.
Правила Хофмейстера были описательными, они не давали причинно-следственных моделей филлотаксиса, хотя и стимулировали их поиск. В частности, правило Хофмейстера, утверждавшее, что новый примордий формируется в месте, наиболее удалённом от остальных, подводило, по крайней мере, неявно, к попыткам представить филлотаксис как задачу оптимальной упаковки дисков на плоскости.
Английский медик Хьюберт Эйри (Airy) (1838 - 1903 гг.) в своей статье.1873 г. "О порядке расположения листьев", опубликованной в трудах Лондонского Королевского общества[40] изложил разработанную им механистическую модель филлотаксиса. Согласно Эйри, все ныне имеющиеся спиральные порядки листьев произошли от одного предкового, а именно, порядка (1, 2), путём сжатия бутона/ побега (вод воздействием внешних условий) и перекручивания оси стебля. В подтверждение Эйри ссылался на проведённые им опыты с шарами, размещёнными на натянутой каучуковой ленте в порядке (1, 2), которые, при ослаблении натяжения и некотором кручении оси, скатывались в спирали, притом имеющие порядки (2, 3), (3, 5) и т.д. Порядков, отличных от фибоначчевских, типа (2, 7) и пр., по словам Эйри, не наблюдалось. Сходство получаемых в опыте результатов с теми, которые наблюдались в природе, было, по мнению Эйри, аргументом в пользу того, что именно так порядки филлотаксиса и образовывались.
Эксперименты Эйри были, вероятно, по большей части мысленными.
Его теория сразу же встретила возражения. Английский ботаник Джордж Хэнслоу-младший в письме в журнал Nature сообщил, что, вопреки мнению Эйри, в природе имеется филлотаксис порядка (2, 7). Хэнслоу сослался на свою статью 1868 г., посвящённую вариациям филлотаксиса у топинамбура (см. далее).
Эйри прислал ответ (письмо в редакцию) на критику Хэнслоу, опубликованный в Nature (10 apr. 1873, pp. 442-443). По поводу наличия в природе порядков 2/7 и пр. он написал, что таковые представляют собой ненормальные случаи. Однако его возражения не затрагивали существа дела – ведь эксперименты, (якобы) проведённые им, вообще не показывали возможности таких порядков. Позже Эйри пришёл к выводу, что появлению таких порядков филлотаксиса, вероятно, произошло под влиянием других факторов, не только внешнего сжатия и скручивания оси (см. Приложение).
Швейцарско-немецкий ботаник Симон Швенденер (Schwendener) (1829 - 1919 гг.) в своей книге 1878 г. "Механическая теория листорасположения" (Mechanische Theorie der Blattstellungen) предположил (возможно, под влиянием идей Эйри), что филлотаксис определяется давлением, или взаимным отталкиванием при контактах между соседними примордиями. Новые примордии в его теории появлялись в наиболее удалённом от других примордий месте, по правилу Хофмейстера.
Появление и распространение дарвинизма стимулировало попытки объяснить филлотаксис адаптацией к условиям жизни и выживанием наиболее приспособленных- естественным отбором. Разработанную концепцию такого рода представил тот же Х. Эйри. В своих письмах к Дарвину 1872- 76 гг. он высказал гипотезу, что все порядки филотаксиса имели своим "предком" порядок (1, 2), т.е. расположение листьев друг напротив друга, и далее, под влиянием внешних воздействий (холода и пр.) стебель скручивался, упаковка примордий становилась более плотной, что давало побегу преимущества при выживании. Такой была, по Эйри, эволюция порядков филлотаксиса.
Дарвин, вероятно, поддержал теорию Эйри; во всяком случае, он представил его статью для публикации в трудах ЛКО.
Вновь возобновились и телеологического характера попытки представить филлотаксис как результат стремления растений к оптимальному по некоторым критериям расположению листьев (теория Эйри также могла быть отнесена сюда – хотя она имела не телеологический, а причинно-следственный характер, но в ней расположение листьев тоже оптимизировалось, по критерию плотности их упаковки в бутоне). Ещё Бонне в работе 1754 г. утверждал, что имеющейся порядок листьев позволяет растению получать максимальный доступ к воздуху.
Новые мотивы к подобного рода рассуждениям добавило открытие в середине- 2-ой половине XIX в. фотосинтеза, процесса преобразования растениями солнечного света в энергию химических связей (термин фотосинтез был введён в 1877 г. немецким ботаником Вильгельмом Пфеффером), и т.о. уяснение важности для растений доступа к солнечному свету.
Австрийский ботаник Юлиус Визнер (Wiesner) (1838 - 1916 гг.) в работе 1875 г. "Флора" (Flora) пришёл к выводу, что расположение листьев по спирали с углом расхождения, равным 360о*(1/t2) даёт им минимальное перекрытие и т.о. является наиболее благоприятным в отношении доступа к свету. Приобретение такой способности Визнер объяснял, в духе времени, естественным отбором. В поддержку своей концепции Визнер проводил эксперименты с освещением листьев, сделанных из бумаги; также он и его последователи полагали, что её можно обосновать строго математически. Через некоторое время она получила название "закона Визнера". Американский натуралист, математик и философ Чонси Райт (Chauncey Wright) (1830- 75 гг.), сторонник и пропагандист дарвинизма в Америке, утверждал, поддерживая концепцию Визнера, что при расположении листьев на генетической спирали согласно золотому углу (360о*(1/t2) » 137°30'28'') последующие не перекрывают предыдущие, доставляя, таким образом, наиболее выгодные условия существования для растения.
Изменение порядка филлотаксиса
Во 2-ой половине XIX в. ботаники накопили много новых фактов, касающихся филлотаксиса. Прежде всего, оказалось, что не все расположения листьев являются регулярными – т.е. числа их парастих (порядок филлотаксиса) не принадлежат к ряду Фибоначчи, и, соответственно, угол расхождения не близок к 137°30'. Далее, обнаружилось, что порядок филлотаксиса у растений одного вида растения может быть разный; более того, даже у одного и того же растения он может измениться по мере его роста – например, порядок (55, 89) у подсолнечника мог смениться на (34, 55) и т.д. Описанием этих явлений, а затем и попытками их объяснения занимались Дж. Хэнслоу-мл., тот же Х. Эйри, С. Швенденер, позже Г. ван Итерсон и другие.
Английский ботаник Джордж Хэнслоу (1835 - 1925 гг.), сын кембриджского профессора Дж.С. Хэнслоу, в статье 1869 г "О вариациях в углах расхождения листьев топинамбура"[41], сообщил, что при изучении расположение листьев на примерно 80 образцах топинамбурв (Jerusalem Artichoke) он обнаружил значительные вариации в их дивергенциях. Порядок 2/5 имели 28% исследованных растений, 3/8 – 40%, 2/7 – 23%. В более поздней статье 1907 г. "Филлотаксис, или расположение листьев согласно математическим законам"[42] он писал, что обнаружил у того же топинамбура не только порядки 1/3, 2/5, 3/8 (фибоначчевские), а также 2/7, но и порядки 3/11, 5/13 и другие. Хэнслоу отметил, что последнюю группу можно было получить, как конечные приближения непрерывной дроби [3, 1, 1, …] – аналогично тому, как первая (фибоначчевская) группа получалась в результате приближений бесконечной непрерывной дроби [2, 1, 1, …]. Вторая группа соответствовало числам ряда Люка.
Хьюберт Эйри после критики, высказанной Хэнслоу в 1873 г. в его адрес, обратился к поиску нерегулярных примеров филлотаксиса, и нашёл их довольно много. В письме Дарвину за 1876 г. он сообщал, что изученные им образцы водяники чёрной (Empetrum nigrum) оказались очень разнообразными в отношении листорасположения: "редкий экземпляр из тех, что мне попадались, не показывал одного- двух переходов от более простого порядка в основании к более сложному в вершине; ещё большим курьёзом являлось то, что этот переход почти всегда был от одного филлотаксического ряда к другому, напр. от первичного 1/2, 1/3, … к другим, напр. вторичному 1/4, 2/7, 3/11 …". Поскольку такие переходы, как считал Эйри, не могли быть осуществлены описанным им ранее процессом сжатия и искривления оси стебля, то он высказал предположение, что за их появлении ответственны другие физические факторы. Изучая эти иррегулрные образцы, Эйри сделал довольно важное наблюдение (позже ставшее основной теорий переходов порядка филлотаксиса): изменение одного порядка на другой происходило из-за некоторого смещения (dislocation) между двумя соседними парастихами.
На случающиеся изменения в порядке филлотаксиса у одного и того же растения, по мере его роста, обратил внимание также и Швенденер. Он связал эти переходы с изменением отношения длины междоуздий к диаметру стебдя (что тоже оказалось существенным в последующих теориях изменения порядка филлотаксиса); так, при уменьшении этого отношения, т.е. при росте диаметра стебля, порядок филлотаксиса (1, 2) переходил в (2, 3), затем в (3, 5) и т.д. При этом, как отметил Швенденер, угол расхождения то уменьшался, то увеличивался (т.к. приближения непрерывной дроби [2, 1, 1, …] сходились к ней то сверху, то снизу, последовательно) стремясь в пределе к углу 360о*(1/t2) .
Во 2-ой половине XIX века среди части ботаников распространилось скептическое отношение к применению геометрии, "игр с фигурами" (историк ботаники Ю. Сакс), для изучения проблем морфологии растений. Тем более, что в то время стали появляться – хотя и очень предварительные – физические и биохимические модели, делавшие попытки дать объяснение характеру роста и расположения листьев у растений.
В начале 1900-х гг. английский ботаник Артур Гарри Чёрч (Church) (1865 - 1937 гг.) в ряде публикаций[43] вновь обратился к построению математических моделей филлотаксиса. Он отметил, что ботаники- его современники нередко просто боятся математики, плохо зная её, но, "подобно тому, как физиология может быть определена как изучение тех эффектов в жизни растений, что подчинены законам физики и химии, так и морфология может быть определена как изучение тех эффектов в живой материи, что подчинены законам Геометрии"[44].
Для описания филлотаксиса, который схематически можно изобразить следующим образом[45]

Чёрч предложил использовать геометрическую модель, в которой боковые вегетативные органы были бы представлены расположенными по спиралям кругами, увеличивающимися в диаметре по мере удаления от центра и вписанными в криволинейные прямоугольники (квази-квадраты, по его выражению)[46].
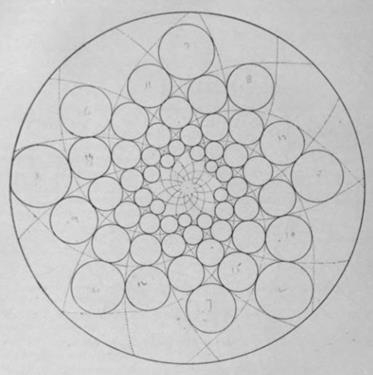
Такие модели гораздо лучше, чем решётки Браве, описывали реальную морфологию растений.
Генетические спирали на схемах Чёрча были менее заметны, чем на решётках Браве. Однако Чёрч считал, что следует отойти от рассмотрения генетических спиралей как первичных объектов, и считать основными два семейства парастихов – которые в предложенном им представлении были хорошо заметными и, кроме того, сохраняли свой характерный спиралеобразный вид.
Критикуя распространённый в его время подход к исследование филлотаксиса через изучение генетических спиралей, Чёрч отмечал, что в ряде случаев – а именно, когда числа левых и правых парастихов имеют общий делитель, отличный от 1 – следует рассматривать несколько спиралей.
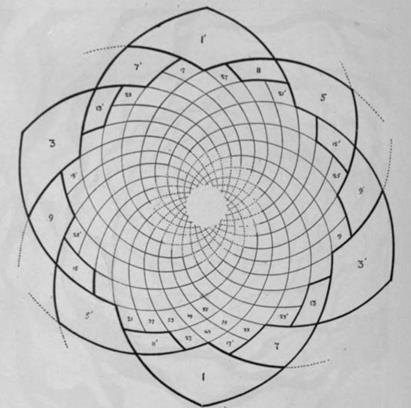
Dipsacus fullonum, порядок спиралей 16:16.
Одним из достоинств своей модели Чёрч считал прояснение положений Визнера о максимуме освещённости для растений при определённом расположения их листьев (на решётках Браве это, конечно, не заметно).
Чёрч считал, что примордии лежат, если не везде, то в регионе вокруг центра, на пересечениях двух семейств ортогональных логарифмических спиралей.
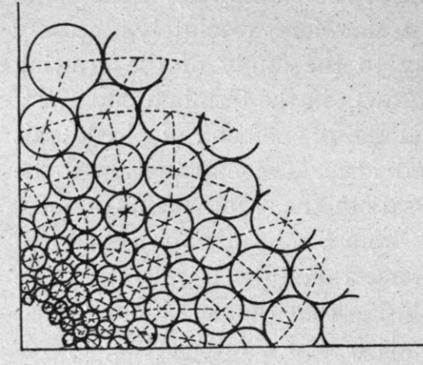
Впрочем, ортогональность спирадей-парастихов имела место далеко не всегда, что сам же Чёрч и отмечал. Свои построения он считал только некоторым идеализированным приближением к реальности.
Чёрч назвал предложенную им геометрическую модель Эквипотенциальной Теорией – имея в виду отмеченную им аналогию между парастихами и линиями равного потенциала в поле статического электричества, а также линиями равного давления в спиральных вихрях жидкости[47]. Впрочем, Чёрч признавал, что его конструкция не даёт никакого причинно-следственного объяснения явления филлотаксиса (op. cit., p. 15) и она является только геометрической моделью для морфологии.
Для объяснения геометрии филлотаксиса и появления чисел Фибоначчи там, Чёрч обращался к теории Визнера, утверждавшей, что при углах расхождения, близких к золотому углу, листья перекрывают друг друга по минимуму и т.о. имеют наилучшее освещение. Он полагал, что Визнер математически доказал это положение – хотя у венского ботаника имелись на этот счёт только относительно правдоподобные рассуждения. Появление у растений способности порождать новые примордии под углом, близким к золотому Чёрч объяснял "внутренним механизмом адаптации"[48], эволюционным приспосабливанием. При этом он считал, что филлотаксис с числами Фибоначчи образовался фплогенетически (эволюционно) раньше, а другие, нерегулярные случаи произошли из него, в результате смещения/ исчезновения части парастихов.
Датский ботаник Геррит ван Итерсон (Iterson) (1878 - 1972 гг.) предпринял дальнейшее изучение проблем филлотаксиса, исходя из идей Браве, Эйри и Хофмейстера. В своей книге 1907 г. "Математические и микроскопо-анатомические исследования филлотаксиса" (Mathematische und mikroskopischanatomische Studien ueber Blattstellungen (Mathematical and Microscopic-Anatomical Studies of Phyllotaxis) он использовал для представления примордий решётки Браве, однако при этом сопоставлял им не точки (как Браве), а круги равных радиусов с центрами в узлах решётки, соприкасающиеся и не перекрывающиеся; то есть, можно сказать, рассматривал их плотную упаковку, в духе идей, предложенных Эйри.
Изображение филлотаксиса с помощью кругов ненулевых размеров на развёртке цилиндра/ на плоскости было ближе к реальности, чем точечное изображение Браве, однако в нём по-прежнему терялась спиральность генетической спирали и парастихов (в отличие от модели Чёрча). Впрочем, для изучения переходов порядков филлотаксиса – чем занялся ван Итерсон – это обстоятельство не было слишком существенным. Хотя размеры примордий и образовывавшихся из них органов были разными (они возрастали при удалении от центра), но изображение их кругами равных радиусов также было в первом приближении допустимым, учитывая, что отображение Браве имело характер логарифмирования по радиусу.
Для прояснения причин изменения, с течением времени, порядка филлотаксиса решающую роль имело наблюдение, которое легче всего можно было сделать в представлении ван Итерсона: при постепенном уменьшении размера кругов, прежде плотная упаковка порядка (m, n) начинает "разуплотняться", и через какое-то время к диску Dk, имеющему на генетической спирали номер k, к которому примыкали сверху, слева и справа, круги Dk+m и D k+n, лежавшие на соответствующих парастихах, примкнёт (слева или справа) диск Dk+m+n с номером k+m+n. Это означает, что порядок филлотаксиса смениться на (m, m+n), или на (n, m+n). При увеличении размера кругов процесс будет обратным.
Все возможные результаты таких переходов можно было изобразить на т.н. диаграмме ван Итерсона – ветвящейся древообразной структуре, в символической форме показывавшей связи между порядками филлотаксиса (а, значит, и углами расхождения) и радиусами кругов.
Изменение размера кругов в представлении ван Итерсона моделировало изменение размеров примордий относительно размеров меристемы, что и происходило у растений. Т.о., диаграмма ван Итерсона показывала, как может меняться порядок филлотаксиса у одного растения с течением времени.
В 1-ой четверти XX в. в ряде работ были отмечены аналогии между симметриями в мире растений и кристаллов
Российский кристаллограф Георгий Викторович Вульф (Wulff) (1863 - 1925 гг.) в своей книге 1908 г. "Симметрия и её проявление в природе" сравнивал филлотаксис с пространственной решёткой кристаллов (стр. 119).
Датский химик и историк химии Франц Мориц Джагер (Jaeger) (1877 - 1945 гг.) в своей книге 1917 г. "Лекции по принципу симметрии и его приложениям в естественных науках" (Lectures on the principle of symmetry and its applications in all natural sciences) также обращал внимание на сходство между филлотаксисом и симметриями у кристаллов. Он выразил мнение, что близость угла расхождения в генетической спирали у растений к фиксированному значению (золотому углу) до некоторой степени напоминает предпочтение гексагональной симметрии в мире кристаллов. Джагер обратил внимание на работу Вульфа, однако, вместе с тем, пришёл к заключению, что такой простой связи между филлотаксисом и симметрией кристаллов, которую предполагал Вульф, не существует, между расположениями органов у живых существ и атомами в молекулах, помимо некоторого параллелизма, имеются и фундаментальные различия.
В 1917 г. шотландский биолог и математик Д'Арси Томпсон (D'Arcy Thompson) (1860 - 1948 гг.) издал объёмистую книгу "О росте и форме" (On Growth and Form), в которой привёл много примеров спиральных форм в живой природе, в т.ч. у растений и моллюсков, а также попытался дать причинно-следственное объяснение этому явлению. Томпсон отметил, что спиральный рост можно представлять как результат взаимодействия двух сил: внутренней силы роста и некоторой "отклоняющей". Если бы эта отклоняющая сила была постоянной и внешней, как, например, ветер для растения, то линия роста, являясь результирующей внутренней силы роста, направленной по касательной, и внешней, имеющей постоянное направление и величину, оказалась бы кривой, но не спиралью – с постепенный выравниванием направления обоих векторов она становилась бы всё более плоской (fig. 239[49]).
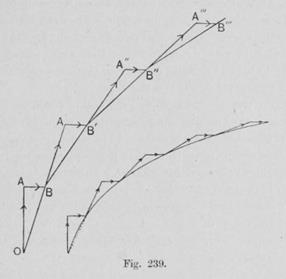
Однако если такая отклоняющая сила была бы внутренней в растущем теле, или так связана с ним в единую систему, что её направление менялось бы вместе с направлением роcта, и если бы она при том ещё была бы перпендикулярна либо наклонена под некоторым постоянным углом к направлению роста, то результатом был бы спиральный рост – что и наблюдается у моллюсков и растений.
Пусть в растущей структуре сила роста F в любой точке P будет действовать вдоль линии, соединяющей P с полюсом О, сила отклонения T будет действовать перпендикулярно к линии OP; и путь отношение величин этих сил p = |F|/|T | будет постоянным в каждой точке. Тогда сила F + T результирующего воздействия будет иметь постоянный угол наклона к радиус-вектору; и, значит,. рост будет происходить по логарифмической спирали. Значение p = |F|/|T | будет определять угол между касательной к спирали и радиус-вектором.
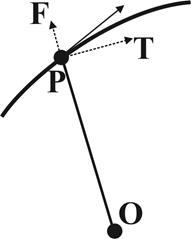
Для раковины моллюска Nautilus такой рост представляет собой непрерывное добавление подобных и увеличенных четырёхугольников, наклоняемых под некоторым постоянным углом к траектории (fig. 242).
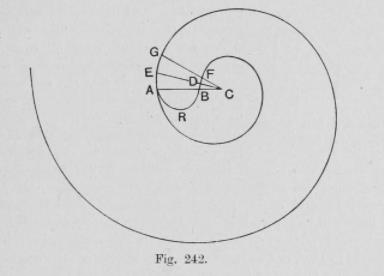
В 1913 г. датский ботаник Иоганн Корнелий Шуте (Schoute) (1877 - 1942 гг.) предложил биохимическую теорию появления филлотаксиса на конусе нарастания: примордии выделяют подавляющее вещество- ингибитор, предотвращающее образование нового примордия слишком близко к ним. Сходные заключения сделал в работе 1948 г. немецкий ботаник Эрвин Бюнинг (Bunning) (1906- 90 гг.): согласно его наблюдениям, стома[50] у растений выделяла вещество, которое препятствовало образованию таких же клеток поблизости. Вывод Бюнинга можно было бы считать определённым аргументом в пользу гипотезы Шуте[51]. Но вскоре английский ботаник Клод Уордлоу (Wardlаw) (1901- 85 гг.) в опытах показал, что примордии развиваются независимо от стимулирующего или тормозящего влияния соседних,. Он надрезал участок, на котором должен был появиться новый примордий, изолировав его таким образом от биохимического контакта с уже образовавшимися примордиями. Тем не менее, новый приморлий появился и развивался как обычно[52]. Затем английские ботаники Кристин Мэри Сноу (1902- 78 гг.) и Джордж Робин Сноу (1897 - 1969 гг.) провели эксперименты, в которых удаляли самый молодой примордий в конусе нарастания у люпина и через две недели определяли положение следующих трёх примордий. Оказалось, что эти новые примордии занимали места, в которых и должны были бы появиться; то есть, их положение не зависело от удаленного примордия и предположительного тормозящего влиянии с его стороны[53]. Итак, следовало искать какие-то иные, не чисто биохимические факторы, определяющие появление примордий в пространстве-времени, а, значит, и филлотаксис.
* * *
В 1948 г. английский ботаник Клод Уордлоу (Wardlаw) (1901- 85 гг.) обнаружил, что каждый примордий создаёт вблизи себя некоторую область напряжений, и высказал гипотезу,, что местом возникновения нового примордия является точка, где эти напряжения достигают минимума[54]. По существу, это было предположение о появлении новых примордий там, где минимизируется некий функционал (напр. энергия). В дальнейшем сходные теории появлялись неоднократно.
* * *
В 1948 г. французский ботаник Люсьен Плантефоль (Plantefol) (1891 - 1983 гг. ) в работе "Теория множественных листовых спиралей" (La Théorie des hélices foliaires multiple) представил новый подход к проблемам филлотаксиса. Игнорируя генетические спирали, он предложил изучать листовые спирали (введённый им термин), выделяемые в расположении листьев на стебле растения (парастихи, не обязательно видимые). Положения новых примордий, возникавших в генеративном апексе, определялись, согласно Плантефолю, листовыми спиралями. Его подход встретил критику, указывавшую на неоднозначность выбора листовых спиралей, и на то, что точки такой спирали не обязательно должны были иметь предполагаемую в рассуждениях Плантефоля сосудистую связь между собой.
* * *
В конце 1940-х – начале 50-х гг. английский специалист в области физиологии растений Фрэнсис Джон Ричардс (Richards) (1901- 65 гг.) в своих исследованиях филлотаксиса вновь обратился к математическому подходу. Он считал, что полное описание филлотаксиса и его динамики дают три параметра: угол конуса, угол расхождения, и введённое им пластохронное отношение (отношение rn+1/rn расстояний последовательно появляющихся примордий до центра апекса). Уравнение генетической спирали с углом расхождения q и пластохронным отношением rn+1/rn будет r = Aebj, где b =(1/q)ln(rn+1/rn). В своей работе 1951 г. Ричардс предложил формулу, связывающую отношение rn+1/rn с числом видимых парастихов, т.е. модой филлотаксиса[55].
Ричардс поддержал гипотезу Шуте о том, что положение примордий определяется биохимическим ингибитором; считал такой подход аналогом "теорией поля".
В схематическом представлении филлотаксиса Ричардс следовал Чёрчу (а не Браве или ван Итерсону):
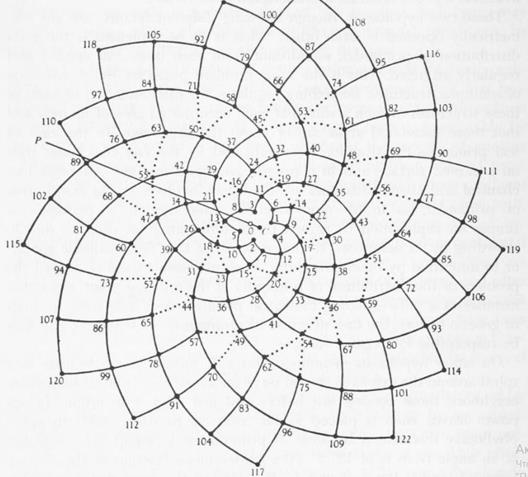
Он отметил, что если по мере роста пластохронное отношение изменяется, то в какой-то момент изменяется и порядок филлотаксиса, и, как следствие, изменяется и угол расхождения генетической спирали. На приведённом примере исходный порядок филлотаксиса (13, 21) через некоторое время перешёл в (8, 13), а затем в (5, 8) (у более молодых)[56].
В то время в изучении филлотаксиса доминировали чисто ботанические описательные методы и Ричардс в своих работах вновь возродил математический подход к проблеме.
* * *
В 1952 г. английский математик Алан Тьюринг (1912- 54 гг.) в работе The chemical basis of morphogenesis[57] предложил теорию самоорганизации филлотаксиса. Согласно ей, морфогенез возникал в результате взаимодействия между ингибитором и активатором.
Модель Тьюринга плохо описывала реальное появление примордий на конусе нарастания, но она стала одной из первых работ по теории самоорганизации; позднее теории такого рода активно применялась в изучении филлотаксиса.
* * *
В 1959 г. французский биолог из университета Пуатье Анри Доффин (Doffin) в своей статье "Филлотаксис и кристаллографические характеристики растений как правильных твердых тел" [58] отметил наличие у растений симметрии, как и у кристаллов, и предсказал, что кристаллографы вскоре обратятся к изучению живых организмов.
В 1960 г. американский ботаник Эдмунд Вэйр Синнот (Sinnott) (1888 - 1968 гг.), профессор Йэля и других университетов, президент Ботанического общества Америки, написал обширную (550 стр.) монографию Plant Morphogenesis, в которой коснулся и проблем филлотаксиса. Он отметил, что по-прежнему остается неизвестным, чем обусловлено возникновение примордий в определенном месте и времени. Синнот считал, что хотя механические и химические факторы влияют на распределение примордий, но предлагавшиеся ранее теории, объяснявшие это распределение тормозящим действием других примордий, размещением в наиболее свободном месте и т.д. не вполне удовлетворительны. По его мнению, появление примордий на генеративном конусе является результатом саморегуляции, за которую ответственны не только перечисленные факторы, но и генетика, и "тонкая структура" протоплазма и пр.[59]. Спиральность, проявляемую в расположениях листьев растений, а также в формах ДНК и других структур органического мира Синном считал "внутренним свойством живого" (deeply seated in the living stuff)[60], что, конечно, не являлось удовлетворительным объяснением этого феномена. Синнот также полагал спиральную симметрию филлотаксиса радикально отличной от симметрий кристаллов и других объектов неорганического мира, а потому поиск аналогий между растениями и кристаллами был, по его мнению, "бесплодным"[61].
* * *
В 1976 г. Джон Торнли (Thornley) в работе Mathematical models in plant physiology, отметив два предыдущих основных подхода к филлотаксису:1) механический – теория упаковки, и 2) биохимический – действие химических веществ, предложил свою модель, относящуюся ко 2-му типу. По ней положение нового примордия определялось изменениями концентрации морфогена, выделяемого уже имеющимися примордиями.
* * *
Аналогию между симметричными структурами в мире растений и у кристаллов несколько нарушало отсутствие у кристаллов пентагональной симметрии, распространённой у растений. Однако, с третьей четверти XX века, после открытия в математике мозаик Пенроуза (с частично пентагонально-симметричным замощением плоскости), а в физике – квазикристаллов (с частично пентагональной симметрией) она вновь приобрела силу.
Мосли Г. О геометрических формах конусообразных и дискоидных раковин, 1838 г.
Хэнслоу-ст. Принципы описательной и физиологической ботаники, 1836 г.
Хэнслоу-мл. О вариациях угловой дивергенции в расположении листьев топинамбура 1869 г.
Хэнслоу-мл. Филлотаксис, или расположение листьев согласно математическим законам 1907 г
Эйри О порядке расположения листьев, 1873; Письмо Дарвину, 1872; Письмо Дарвину, 1876 г.
Мосли Г. О геометрических формах конусообразных и дискоидных раковин, 1838 г.[62]
Поверхность любой дискоидной или конусообразной (turbinate) раковины можно представить как результат вращения вокруг оси раковины фигуры, расширяющейся во всех измерениях и при этом всё время остающейся подобной самой себе. Для дискоидных раковин порождаемая при вращении фигура будет находиться в той же плоскости, например, у моллюсков Nautilus Pompilius или у Argonaut. Для конусообразных она будет непрерывно скользить вокруг оси вращения. Для многих семейств моллюсков, таких как Ammonites, Nautilus scrobiculatus, Nautilus spirula, Helix cornea, Trochus, порождаемая фигура по мере увеличения расстояния от оси, одновременно вращается и увеличивается в размерах.
Среди конхоидальных (греч. κόγχη – раковина) поверхностей можно найти самые разные геометрические фигуры. У Conus Virgo это треугольники, у Trochus telescopicus и Trochus Archimedis – трапецоиды. У видов рода Turbo формы будут круговыми и эллиптическими, для периметров которых образующие конуса являются касательными. Nautilus Pompilius порождается вращением вокруг его короткого диаметра плоской кривой, примерно полуэллипса, а Cyprsea – вращением сходной кривой вокруг его более длинного диаметра.
Заметно сходство (mechanical uniformity) в строении раковин одного и того же вида, из чего можно заключить, что каждая из них спирально расширяется по некоторому общему простому геометрическому закону (p. 351).
Эта спираль всегда является логарифмической. Только взглянув на неё можно заключить, что угол, под которым она пересекает радиус-вектор, постоянен, что соответствует определению логарифмической спирали (p. 352).
Хэнслоу-ст. Принципы описательной и физиологической ботаники, 1835 г.[63]
Английский ботаник Дж. Хенслоу-старший (1796 - 1863 гг.), с 1823 г. профессор Кембриджа, в своём учебнике 1835 года упоминал о спиральном расположении листьев растений и чешуек сосновых шишек, о боковых спиралях, углах расхождения у генетической спирали. Он приводил для ряда растений эти параметры, а также другие результаты по филлотаксису, описанные в недавних (начала 1830-х гг.) работах Шимпера и Брауна.
Если мы проведём линию от любого листа к соседнему вверху и так далее, то, даже в случае, когда листья весьма разбросаны по растению, эта линия представит собой спираль. В конечном счёте мы придём к листу, расположенному вертикально над исходным. Обычно считали, через сколько листьев очередной окажется над исходным, не учитывая, сколько при этом получится оборотов. Так, на рис. 136 A это будет один оборот, на 136 B – три оборота, или витка спирали.
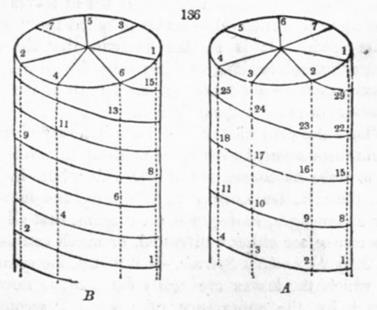
М-р Браун предложил обозначать такие расположения числами, через которые можно было бы выразить угловое расхождение между двумя последовательными листьями, если их спроектировать на плоскость, перпендикулярную оси (стеблю). Эта величина получила название (угла) расхождения генетической спирали.. Так, расхождение в случае A представляет собой угловое расстояние между 1 и 2 (т.е. 1/7 окружности); а для случая B – 3/7. Числители этих дробей равны количеству витков, которые сделает генетическая спираль, до того, как очередной лист окажется вертикально над исходным, а их знаменатели равны количеству листьев в этом участке спирали. Листья в наших примерах группируются по вертикали в 7 параллельных рядов (ортостихов).
Если витки спирали не слишком близки друг к другу, то путь (генетической) спирали вокруг оси проследить легко, но во многих случаях витки оказываются так близки между собой, а листья или другие придатки так расположены на них, что её путь скрытен или сильно запутан.
Но симметрия в расположении листьев всегда проявляется во "вторичных" спиралях, которые могут быть прослежены в разных направлениях. Они хорошо видны в порядке устройства чешуек еловых шишек (рис. 137)[64]; и мы постараемся показать, как размещение чешуек на генетической спирали может быть легко определено из изучения этих вторичных спиралей. Так, у шишек елей Pinus abies нетрудно увидеть спирали, параллельные чешуйкам с номерами 1, 9, 17, 25, &c.; и другие спирали, параллельные 1, 6, 11, 16, &c.; также 1, 4, 7, &c., и т.д. В этом примере имеется 21 линия, которую можно провести через чешуйки, находящиеся одна над другой, именно 1, 22, 43, &c., 14, 35, 56, &c. и т.д. Это число, как и 7 вертикалей на рис. 136B, указывает на количество чешуек, приходящихся на один виток спирали. Но здесь, конечно, генетическая спираль не видна, и, следовательно, числитель в дроби, выражающей угол расхождения, неизвестен.
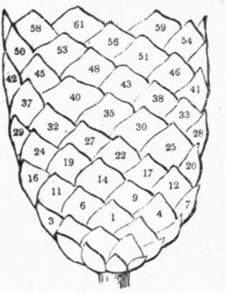
Нетрудно заметить, что номера чешуек, образующих вторичные спирали, составляют арифметические прогрессии, притом, как мы покажем далее, шаг этих прогрессий равен числу вторичных спиралей, параллельных между собой. Так, в вышеприведённом примере имеется 8 параллельных спиралей: 1, 9, 17, &c., 6, 14. 22, &c., у которых шаг прогрессии равен 8. Значит, у нас есть метод нумерации чешуек на шишке без обращения с генетической спирали. Начнём с чешуйки (1) и, подсчитав количество параллельных спиралей, имеющих одно направление (здесь 8), мы можем приписать числа 1, 9, 17, &c. на одной из этих спиралей. Затем, подсчитав число спиралей, имеющих другое направление (здесь 5), мы можем приписать им числа 1, 6, 11, &c. Так будут пронумерованы все чешуйки. Генетическую спираль образуют чешуйки с номерами 1, 2, 3, &c. Нетрудно подсчитать число параллельных спиралей одного класса внутри какого-нибудь сегмента, рассматривая, сколько пересечений они имеют с окружностью сегмента. Так, спираль 1, 6, 11, 16 ... 38, 46, 51, 56 имеет 4 параллельных ей; всего таких 5. На обрезанном крае мы видим то же, именно 5 спиралей, проходящих через чешуйки с номерами 54, 59, 56, 6l, 58, &c. Но даже и не занумеровывая много чешуек, мы можем установить вначале знаменатель, а потом числитель дроби, выражающей расхождение. Нам нужно только взять в одном направлении 1, 9, 17, а затем пройти от 17 к 22 в другом направлении, и мы прибудем к чешуйке, находящейся над 1. Т.о. знаменатель нашей дроби будет 21. Чтобы найти числитель, возьмём чешуйки 2 и 23, последняя расположена вертикально над первой, и подсчитаем, сколько чешуек лежит между вертикалями (1, 22,) и (2, 23) – это будут чешуйки с номерами 9, 17, 4, 12, 20, 7, 15, через каждую из которых проходят свои вертикали. Мы получаем, таким образом, числитель 8, а значит, расхождение для генетической спирали будет 8/21. Возможно, это лучше видно на рис. 138, в котором указана относительная позиция чешуек на одном витке спирали.
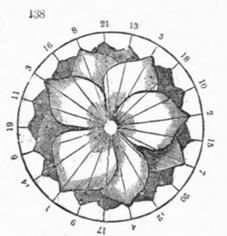
Хотя число вторичных спиралей, которых можно легко различить, ограничено, но очевидно, что мы можем провести спираль с любым шагом, просто начав с номера 1 и далее отмечая чешуйки с номерами с этим шагом. Одни из таких спиралей будут левозакрученными, другие – правозакрученными. Число спиралей одного класса будет равно шагу прогрессии. Генетическая спираль, проходящая через элементы с номерами 1,2, 3, &c., единственна. Вторичная спираль, проходящая через элементы с нечётными номерами 1, 3, 5, &c., оставляет элементы с чётными номерами, 2, 4, 6, &c., которые образуют вторую спираль того же класса; т.е. есть две вторичных спирали с шагом 2. Аналогично, есть 3 спирали, проходящие, с нагом 3, через элементы с номерами 1, 4, 7, &c., 2, 5, 8, &c., 3, 6, 9, &c. и т.д.
Вариации в углах расхождения. Расположение листьев на одной части растения может подчиняться одному закону расхождения, а в другой части, или для другого растения, даже того же вида – другому закону. Так, у нескольких шишек с одной ели иногда бывают разные углы расхождения. Много таких аномалий происходят из-за отклонений , которые нетрудно заметить – искривлений оси, потери части &c. Также довольно обычно встретить на одном и том же растении генетические линии разных направлений.
Примеры расхождений. Из вышесказанного легко видеть, что расположение листьев на растении определяется генетической спиралью, кроме, конечно, иррегулярных случаев, когда потеряны все следы симметричного порядка. Так, когда придатки располагаются в линию по одной стороне оси (стебля), расхождение будет 1/1; когда они лежат в двух противоположных рядах – (рис. 139) расхождение будет 1/2, когда в три ряда – 1/3, или 2/3, последний, впрочем, может рассматриваться как тот же 1/3, только с поворотом вокруг оси в другом направлении. Одним из самых частых является пятикратный (quincunxial) порядок, при котором листья, или цветки расположение в пять рядов. Он может быть произведён 4-мя различными расхождениями, представленными на кругах в рис. 140; здесь также видно, что два из них такие же как и другие два, только идущие в обратном направлении. Если знаменатель простое число, то дивергенций для такого расположения (т.е. видов генетических спиралей) будет на 1 меньше. Но если знаменатель не есть простое число, то некоторые из дробей, представляющих расхождения, дают те же спирали, что и дроби с меньшими знаменателями. Так, если имеется 6 вертикальных рядов (рис. 141), то дивергенции могут быть 1/6, 2/6, 3/6, 4/6, 5/6, но 2/6 = 1/3, а эта дробь представляет собой генетическую спираль с тремя витками; 3/6 = 1/2, а эта дробь представляет генетическую спираль с лежащими напротив друг друга листьями.
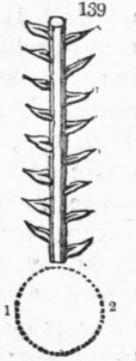
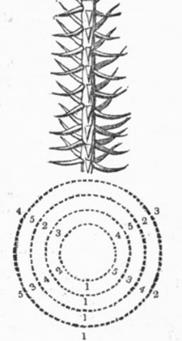
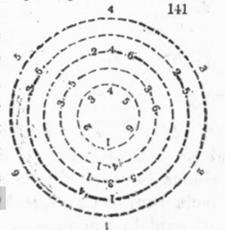
Примеры разных дивергенций среди некоторых видов растений из следующих родов, взятые из таблицы, приведённой м.-ром Брауном,
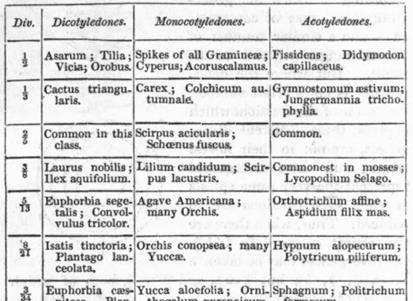
К этому списку мы добавим сложный пример – группу колючек- инволюкр[65] чертополоха шерстистого (Carduus Eriophorus), и покажем, как можно получить для неё расхождение. Легко заметить у них два набора спиралей, параллельных, соответственно AB и CD (рис. 142), здесь первых 34, а последних 21. Взяв №№ 1, 35, 69, в одном направлении и 90,в другом, мы получим бракты, которые находятся вертикально над №1. Бракт №35 лежит, очевидно, ниже любого другого бракта, расположенного на вертикальной линии, проходящей через 1 и 90. Чтобы построить фигуру, представляющую виток генетической спирали, сделаем следующее. Поместим №1 на окружность (рис. 143), и разделим её на 89 равных частей; поместим №35 рядом с №1: 34 – это шаг данной вторичной спирали, на ней находятся №№ 1, 35, 69, 103, &c., из которых мы поместим 69 вслед за 35; но 103 уже находится на втором витке генетической спирали; вычтем из него 89 и получим 14, который лежит на вертикали под ним, и находится т.о. внутри первого витка генетической спирали, и значит, предшествует 69 на окружности. От №14 начнём вторую спираль, шагом которой будет такой же (35), значит, мы поместим №№ 48, 82, вслед за 14, а 106 уже выходит за пределы первого витка генетической спирали; снова вычитаем 89, что даёт 17 для следующего числа на окружности. И так делаем, пока не прибудем к №2.
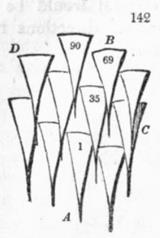
Мы обнаружим, что №2 находится на 55-м интервале от №1, и, следовательно, число 55/89 и будет расхождением для данного примера"[66].
Хенслоу-мл. О вариациях угловой дивергенции в расположении листьев топинамбура[67].
Изучая расположение листьев на примерно 80 образцах топинамбурв (Jerusalem Artichoke) я обнаружил значительные вариации в их дивергенциях. Наиболее частыми были следующие:
2/5 – в 28% исследованных стеблей
3/8 – в 40%
2/7 – в 23%
Хенслоу-мл. Филлотаксис, или расположение листьев по математическим законам[68].
Я нашёл у топинамбура (Jerusalem Artichoke) множество вариаций в расположении листьев – в отличие от большинства других видов растений, сохраняющих характерный для них порядок неизменным. У него были не только противоположные пары, но также сгруппированные тройками … кроме того, листья на многих стеблях были расположены в порядках, представленных дробями 1/3, 2/5, 3/8 и т.д. Более того, я обнаружил, что у него нередко встречаются дивергенции согласно дробям 2/7, 3/11, 5/13 и другие. Последние представляют собой часть вторичного ряда, который может быть продолжен так: 1/3, 1/4, 2/7, 3/11, 5/18, 8/29 и т.д. Этот ряд можно получить, поставив на первые места 1/3, 1/4 вместе 1/2, 1/3 и вычисляя следующие дроби по правилу сложения между собой числителей и знаменателей.
Точно так же, как все угловые расхождения листьев для первого ряда лежат между 120° и 180° включительно, для вторичного ряда они оказываются между 90° и 120°, границей будет 99°30' 6".
Следует отметить, что дроби вторичного ряда представляют собой приближения непрерывной дроби [3, 1, 1, 1, ….].
Аналогичным образом мы можем сконструировать третичный ряд, начав его с дробей 1/4, 1/5, и получая далее 1/4, 1/5, 2/9, 3/14, 5/23, 8/37, &c. Более того, дивергенции с дробями из этого ряда и других встречаются в природе, именно, у плаунов (Lycopodium) есть дивергенции с дробями 2/7, 2/9, 2/11, из рядов 1/3, 1/4, &c, 1/4, 1/5, &c, 1/5, 1/6 соответственно. Хотя такие случаи сейчас не часты, но интересно отметить, что в каменноугольный период встречались деревья из семейств, близких к нашим плауновым, с такими расположениями листьев. Я нашёл порядок 2/7 на ветке у Araucaria imbricata, хотя обычный порядок у них принадлежит первому ряду – 1/2, 1/3, &c. Это хвойное дерево является представителем очень древнего типа. Имея три похожих ряда, ясно, что мы можем сконструировать и другие такие же ряды, которые будут представлены приближениями непрерывных дробей [а, 1, 1, 1, ….].
Из этих наблюдений вытекает правило получения дроби, задающей угловое расхождение т.н. генетической спирали. Правило: сумма двух номеров вторичных параллельных спиралей, здесь 13 + 8 = 21, образует делитель, а меньшая, т.е. 8, образует числитель, т.о. 8/21 представляет угловое расхождение генетической спирали. Из этого ясно, что вертикально над чешуйкой №1 находится №22, начинающая новый круг.
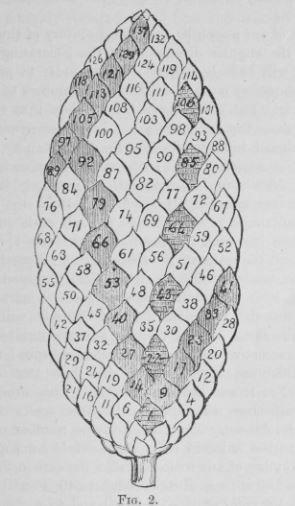
Метод нумерации чешуек. Пусть у нас есть 8 параллельных вторичных спиралей направо, и 13 налево (см. рис. 2), Тогда можно приписать каждой чешуйке на шишке свой номер следующим образом.. Начнём ч №1 и припишем числа 1, 9, 17, 25, 33, 41, 89, 97, 105, &c. чешуйкам на вторичной спирали, проходящей от №1 направо; эти номера представляют собой арифметическую прогрессию с шагом 8, или числом параллельных спиралей. Аналогичным образом припишем числа 1, 14, 27, 40, 53, &c. на последовательных чешуйках вторичной спирали, идущей налево, с её шагом 13. Т.е. мы получим две вторичных спирали, пересекающихся в №1, а затем снова в №105, у которых каждая чешуйка пронумерована. Аналогичным образом нумеруем чешуйки всех других спиралей. Когда это будет проделано, можно увидеть, что над номером 1 находится чешуйка с номером 22.
Имеется 21 вертикальный ряд чешуек (ортостихи). Это можно без труда увидеть, установив шишку горизонтально и рассматривая ряды, параллельные оси.
Хотя, как было сказано выше, 22-я чешуйка находится над 1-й, но не точно над ней, а с некоторым отклонением. Это ясно из того, что 8/21 от 360°, т.е. 137°31', не является кратной частью окружности, и потому 22-я чешуйка немного отклоняется по вертикали от 1-й[69]. 43-я удваивает это отклонение, 64-я утраивает и т.д. Т.о. предполагаемая вертикальная линия на самом деле оказывается ещё одной спиралью (парастихом), и мы имеем, вместо 21 вертикального ряда 21 весьма крутую (почти прямую) спираль.
Чтобы ряды на стебле были строго вертикальными, порядок должен представляться дробями, у которых знаменатель является делителем 360°, такими как 1/2, 1/3, 2/5, 3/8; в то врем как 5/13, 8/21 &c. дают спирали, у которых ни один лист не находится строго вертикально над другим.
Обычно порядок листьев на стебле с хорошо развитыми междоузлиями представляется одной из следующих дробей –1/2, 1/3, 2/5, 3/8; а порядок на стебле с недоразвитыми междоузлиями, как напр. чешуек на сосновой шишке представляется дробями 5/13, 8/21, 13/34 &c.
Эйри Хьюберт О порядке расположения листьев[70].
27 февраля 1873 г. Уильям Споттисвул, M.A.[71]. зачитал следующее сообщение:
"О порядке расположения листьев" Хьюберта Эйри (Airy), M.A., M.D.
Представлено Чарльзом Дарвином, , F.R.S. Получено 21 января 1873 г.
Полагая известными следующие основные факты о расположении листьев – они делятся на кольцевые и спиральные типы, притом порядок последних представлен членами сходящегося ряда дробей 1/1, 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, 34/89, 55/144, &c. – можно спросить: какой за этим скрывается закон?
М-р Дарвин приучил нас рассматривать разные виды растений как потомков общего предка; и т.о. мы можем предположить, что разные расположения листьев, существующие ныне, произошли из некоторых модификаций определённого предкового расположения.
Один спиральный порядок мог переходить в другой в результате кручения оси, вокруг которой расположены листья. Такими способами – именно, поворотами оси на разные градусы – разные спиральные порядки могли произойти от первичного.
Естественно принять простейшее расположение листьев в два противоположных ряда, 1/2, как самое близкое к исходному; порядки в других случаях (чешуек на сосновых шишках, цветочков в головках астровых (Compositœ), листьев подорожника &c.) являются специализированными и высокоразвитыми; несомненно, они представляют собой позднейшие ступени филлотаксиса; и мы можем быть уверены, что изменения шли от более простых к более сложным, а не наоборот. Эта точка зрения будет проиллюстрирована далее.
Но вначале зададим вопрос: зачем нужны эти порядки? И в какое время жизни растения они дают ему преимущество? Расположение листьев должно быть наилучшим не тогда, когда ветки достигли зрелости, с большими междоузлиями между листьями, а когда ветки и листья ещё только содержатся в зачаточной форме в почке; т.к. там порядок листьев не нарушен искажениями или неравенствами роста; ведь, по мере раскрытия зачатка в ветку, листья разделяются, стебель частично искривляется, листья поворачиваются, чтобы их поверхность имела лучший доступ к свету; т.о. порядок, который был в зачатке или бутоне, становится скрытым в выросших образцах.
Для бутона мы сразу видим, в чём может быть польза порядка листьев . Это экономия места, из-за чего бутон может быть сжатым и оставлять наименьшую поверхность для внешних опасностей и превратностей изменений температуры. Тот факт, что порядок 1/2 не показывает такого преимущества, поддерживает идею, что этот порядок является исходным, из которого произошли более сложные.
…
То, что порядок 1/2 мог при разных степенях сжатия и искривления давать последовательно разные спиральные порядки, которые существуют в природе, в порядке их усложнения, 1/3, 2/5, 3/8, 5/13, &c., показывает следующий эксперимент.
Возьмём некоторое число шаров (скажем, чернильных орешков (oak-galls)), которые будут представлять зачатки листьев, и расположим их в два ряда друг напротив друга (порядок 1/2) на противоположных сторонах натянутой ленты из каучука (индийской резины). Слегка повернём ленту, чтобы определить направление искривления и дальнейшего сжатия, и ослабим натяжение. Два ряда шаров скатятся в спирали, порядок которых будет близок к 1/3. Если шары установлены немного дальше от оси, то порядок будет около 2/5, с большой устойчивостью. Представляется (it appears)[72] что дальнейшее сжатие, с увеличением расстояния между шарами от оси, произведёт порядки, последовательно, около 3/8, 5/13, 8/21, &c., и что эти последовательные порядки будут наиболее устойчивыми состояниями в процессе изменения от простейшего к сложному.
Представляется также, что порядки, возникающие в процессе сжатия, необходимо исключает, как несуществующие, дроби 1/4, 2/7, 3/7, 4/9, 4/11, &c.
Изучение спиралей семян в головке подсолнечника и другие примеры, дают удивительное согласие с вышеприведённым процессом. Его крайнее семечко, обозначенное как 0, находится в контакте с 34-м, 55-м, и 89-м (считая в порядке роста), и даже с 144-м. Одуванчик, с меньшей степенью сгущения семян, имеет 0-й в контакте с 13-м, 21-м, и 34-м в крупных экземплярах; домашний лук-порей имеет в своём порядке листьев 0-й в контакте с 5-м, 8-м и 13-м; у яблок наблюдаются 0-й в контакте с 2-м, 3-м, 5-м, т.о. мы видим в природе те же ряды в контакте с 0-м, что мы и в эксперименте[73].
Различие порядков у близких видов (напр. Plantago major и P. coronopus) тесно связано с различиями в их потребностях и поведении.
Доминирование порядка 1/2 у морских Algœ и у Gramineœ, низко развитой стадной группы, и их слабая варьируемость, в отличие от вариаций, наблюдаемых у разных экземпляров вяза, бука и пр., поддерживают утверждение, что порядок 1/2 – исходный для спиральных.
У многих растений мы находим переходы от порядка 1/2 к более сложным, напр. посевной каштан (Spanish chestnut), лавр, орех, плющ имеют высокий порядок в большинстве побегов, и в то же время в менее заметных боковых они сохраняют простой порядок 1/2. Несколько сортов алоэ имеют порядок 1/2 в своих нижних листьях и более высокий порядок у оставшихся. Виды кактуса часто содержат полный набор порядков в одном растении, или даже одном побеге.
Превалирующее двухрядное устройство корнеплодов и корней, видимо, является пережитком в подземной части порядка, который ранее доминировал у всего растения, в его корнях, стеблях, ветвях.
Во всём классе однодольных растений первые листья у зародышей имеют порядок 1/2.
В классе двудольных первые листья у зародышей имеют простейший мутовчатый порядок[74].
Как спиральный порядок произошёл от двурядного, так и мутовчатый порядок, вероятно, произошёл от двурядного коллатерального (лист + боковой побег; два рядом) расположения. Это показывает опыт, аналогичный вышеприведённому.
…
Причиной исчезновения двухрядного коллатерального порядка, вероятно, является его неустойчивость; т.к. при боковом давлении он переходит в двурядный противоположный, а при вертикальном – в перекрещивающийся.
Бутон получает свою устойчивую форму под воздействие сил сокращения, сжатия и роста.
Суммируя, мы приходим к заключению, что прототипом всех существующих порядков листьев был двурядный, возможно, в двух модификациях – противоположной и коллатеральной; и что противоположная дала начало всем спиральным, а коллатеральная – мутовчатым порядкам, в результате приспособительных сжатий на протяжении веков.
Эйри Письмо Дарвину, 1872. July.
…
4. Поставим теперь вопрос, какие у нас есть свидетельства, указывающие на порядок 1/2 как на предковый. Тот факт, что он является простейшим, не слишком важен, разве что как намёк, показывающий в каком направлении нам следует двигаться, поскольку вполне допустимо, что сложные структуры могли быть более ранними, если сложность относится не к организации, а к форме.
Куда важнее тот факт, что порядок 1/2 доминирует у злакоцветных (Gramineæ), которые являются теплолюбивыми, стадными (gregarious) и низкоразвитыми, в то время как у елей, которые являются преимущественно высокогорными (alpine) по своим местам обитания, и холодостойкими в высоких широтах, мы находим очень высокую плотность листьев, чешуек или иголок. Проследить условия, из-за которых вязы в нашей температурной зоне сохранили порядок 1/2, в то время как тропические папоротники приобрели порядки, по сложности соперничающие с порядками хвойных деревьев, было бы трудной, но в высшей степени интересной задачей. Для этих и других аномалий, очевидно, следует искать факторы воздействия, отличные от холода. В случае папоротников жара также могла быть врагом, как у тропических луковиц и других. Многие звездоподобные растения, которые лежат прямо на земле и таким образом избегают жвачных животных и других своих травоядных врагов, возможно, приобрели эту многолучевую сложность под влиянием таких угроз, против которых низкие стебель и зачатки давали преимущества.
Нет недостатка в примерах растений с оставшимся/ выжившим простым порядком 1/2: вяз, бук, липа, шелковица и разные травы, насколько я мог наблюдать, практически не отклоняются от него. Однако есть ли примеры перехода от 1/2 к более сложным? Да, и много, это весьма важный и интересный факт. Одним из таких растений является каштан посевной у которого, по крайней мере, в боковых ветвях, первые полдюжины листьев расположены в порядке 1/2, а остальные следуют порядку 2/5 или близки к нему. То есть (я так интерпретирую этот факт) верхушка почки, в течении веков, чувствовала надобность в сжатии, для противодействия холоду, в то время, как у нижней части побега, закрытой и защищённой верхними ветвями, остался прежний исходный порядок 1/2.
Такое же явление наблюдается у лавровишни португальской; однако здесь, как правило, не ранее чем через 2-3 года роста крайние побеги на боковых ветках оставляют порядок 1/2 и переходят к 2/5, впрочем, в отдельных случаях порядок 2/5 на листьях боковых ветвей можно наблюдать уже в первый год.
У лавровишни лекарственной только когда крайний побег на боковых ветвях становится головным, листья на нём оставляют порядок 1/2 и переходя к 2/5. Отвесные главные побеги часто имеют порядок 2/5 с самого начала.
У ореха отвесные листья обычно располагаются в порядке 2/5, а боковые ветви в порядке 1/2. У плюща ползущие по земле или вдоль стены части имеют порядок 1/2, но когда они ветвятся в воздухе, то их порядок 2/5 или более сложный.
В приведённых примерах общим является расположение в сложном порядке у тех побегов, которые занимают самые открытые места, и сохранение (предположительно) предкового порядка 1/2 у менее открытых, боковых побегов.
Обычный тепличный кактус часто проявляет целый набор разных расположений на одном растении или даже на одном побеге. Однако у него их порядок обратный – в нижней части он наиболее сложный, например, 8/21, выше переходит в 5/13, 3/8, 2/5, 1/3, и наконец, на вершине, становится плоским, с порядком 1/2. Здесь. видимо, самой ранней и древней части бутона больше всего требовалось сжатие: не было стебля, способного предотвратить уход от старого простого порядка 1/2; но более молодая часть, не подвергавшаяся таким опасностям, как старые, и, видимо, сформировавшаяся при более тёплой погоде, вернулась к (предположительно) предковому порядку 1/2. …
6. Я полагаю, что дополнительные свидетельства того же явления представляют расположения частей у корнеплодов или корней. Многие растения, такие как редис, шпинат, свекла, коровяк, осот, пастушья сумка, крестовник, чёрный паслён, &c., листья которых располагаются в порядке 2/5 или 3/8 (приблизительно), имеют два ряда корешков на главных корнях, часто с явным разделением у верхушки. (Обычный щавель имеет три ряда, пастернак и морковь имеют четыре, вероятно, эти случаи можно рассматривать как две пары рядов. Помимо подобных исключений, насколько я мог наблюдать, у корешков доминирует двойной порядок). Эти два ряда у корешков соответствуют первой паре листьев на стебле внизу. Наличие некоторого древнего сходства между стеблем растения и корнем показывает и почкование от корней у отдельных растений, и отделение корешков от стебля у других.
Предполагая, что листья и корешки некогда имели один и тот же порядок расположения, мы можем увидеть причину, почему у первых порядок изменился (на более сложный), в то время как у последних он остался прежним. Эта причина состоит в том, что корни, будучи укрытыми в земле, не подвергались таким опасностям на протяжении веков как находящиеся над землёй растения. Неожиданные изменения температуры, от полуденной жары до полуночных заморозков, под землёй сглаживались, и корень не имел надобности упаковывать свои корешки более плотно, в закрытый и защищённый бутон, способный противостоять пагубным изменениям. Далее, корешки не подвержены случайным ударам. По сути, единственным сходством (у листьев и корешков) была надобность "удобного и быстрого" распространения вокруг стебля, которую м-р Чонси Райт (Chauncey Wright) считал столь важной для обеспечения возможности получения пищи из окружения, и действия, происходящие из этой надобности, скорее всего, были бы одинаковы в обоих случаях. Мы можем т.о. ожидать, что найдём сохранённый старый порядок, или, по крайней мере, указания на него, в расположении корешков на корне; в то время как порядок листьев на стебле следует считать результатами борьбы в течении миллионов лет с невзгодами и трудностями жизни над землёй.
"Старый порядок меняется, уступая место новому"[75]
(далее описание эксперимента, приведённого в статье 1873 г.)
…
Коротко говоря, единственные устойчивые порядки, которые могут образоваться сжатием системы, это те, которые определены рядами (1/2. 1/3): 2/5, 3/8, 5/13, 8/21 &c.: и именно они встречаются в природе. …
Эйри Письмо Дарвину, 2 May 1876.
…
В моей новой статье содержится описание порядка листьев у водяники чёрной (Empetrum nigrum) и обсуждение его отношения к общей проблеме расположения листьев. Веточки этого растения удивительно разнообразны: редкий экземпляр из тех, что мне попадались, не показывал одного- двух переходов от более простого порядка в основании к более сложному в вершине; ещё большим курьёзом являлось то, что этот переход почти всегда был от одного филлотаксического ряда к другому, напр. от первичного 1/2, 1/3, … к другим, напр. вторичному 1/4, 2/7, 3/11 … Такие переходы не могли быть осуществлены процессом сжатия, и я хотел понять, как они произошли.
…
У 46 из 50 образцов имел место переход от порядка из одного ряда к порядку из другого ряда, и там, где можно было проследить детали, причиной этих переходов была любопытная иррегулярность, которую я назвал спиральным смещением между двумя соседними вторичными спиралями. Результатом такого смещения являлось полное расстройство рядов, не принадлежащих к этим спиралям, и появление на их месте нового множества спиралей (с другими числами порядков), производя т.о. полностью новое расположение листьев.
…
Из этого факта вытекает, что значение, придаваемое в некоторых учебниках по ботанике "генетическим" спиралями преувеличено. Для водяники чёрной такие спирали, видимо, не более важны, чем другие геометрические ряды; они прерываются при каждом переходе, и вместо них появляются новые, притом движущиеся в противоположном направлении.
Единственное описание чего-либо подобного для изменения порядка листьев встретилось мне в статье Revd. G. Henslow (Trans. Linn. Soc. vol. XXVI p. 647) "On the Variations of the Angular Divergences of the Leaves of Helianthus tuberosus". Вариации расхождений у этого растения представляются имеющими такой же характер, что и вариации у Emp. n., только гораздо более ограниченными по диапазону.
Философия
Западная философия использовала образ спирали для описания принципа эволюции; например: развитие общества "совершается по спирали", проходя через некоторое время "ту же" точку, на более высоком уровне. "Всё существующее движется и развивается по спиральному пути" (И.А. Ефремов).
В китайской философии символом дао – колебательного пути мира: "один инь, один ян, один инь, один ян,…" – считалась двойная спираль. Изображения спиралей встречались в даосских текстах.



Рисунки из собрания даосских текстов "Дао Цзан"
Напоминает спираль и символ Великого Предела – инь+ян.

Спирали присутствуют, явно или неявно, во многих объектах.
Для обозначения бесконечности шотландский математик Валлис XVII века ввёл символ ∞, напоминающий двойную спираль.
При изображении дао как "один инь, один ян, один инь, один ян,…", с учётом инь= 6; ян= 9., несколько загадочным образом получается спираль:
Смотри!
Магические квадраты порядка 3 и 5. Если расположить числа 1-9 последовательно по трём концентрическим кругам (см. рисунок справа), то числа в строках и в столбцах магического квадрата 3*3 окажутся лежащими на спиралях, как бы выходящих из центра, подобно спиральным линиям на подсолнечнике (см. рисунок выше.). Для квадрата 5*5 аналогично.