Числовой октаэдр и его симметрии

 

геометрические объекты и их группы симметрий

   квадрат; правильный восьмиугольник; двойная пирамида

числовой октаэдр и его группа симметрий

триграммное представление числового октаэдра

квазисимметрии расположений числового октаэдра

симметрии в расположениях триграмм

 

Рассматривается числовой октаэдр – набор {3ⁿ, 2ⁿ} (mod 10), в котором вводится операция ¤-умножения, превращающая его в группу, изоморфную группе симметрий квадрата. Вводится понятия квазисимметрий и рассматриваются квазисимметричные представления групп для расположений числового октаэдра в пространстве.

 

Геометрические объекты и их группы симметрий

 

Группа симметрий квадрата

Пусть A₁, A₂, A₃, A₄ – вершины квадрата, l₁, l₂, l₃, l₄. – его оси симметрии.

Рис I.1.

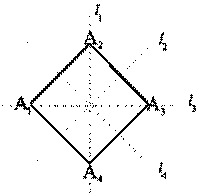
Рассмотрим группу симметрий квадрата. Она состоит из 8 элементов: 4 поворота вокруг центра, на углы 0, π/2, π, 3π/2, и  4 отражения вокруг осей l₁, l₂, l₃, l₄. Обозначим ее C₈. Набор вершин квадрата {A₁, A₂, A₃, A₄} будем обозначать A₍₄₎.

Пусть g – поворот квадрата на π/2 по часовой стрелке; ε – отражение квадрата около оси l₁. Тогда повороты будут представлять собой преобразования gⁿ (n = 0, 1, 2, 3). Очевидно, что g⁴   = e. Очевидно, g и ε – образующие группы C₈; C₈ = {e, g, g², g³, ε, g*ε, g²*ε, g³*ε}.

Лемма I.1. g^n–1*ε = отражение вокруг l_n (n = 1, 2, 3, 4).

Т.о. все отражения являются преобразованиями gⁿ*ε (n = 0,..,3).

Лемма I.2. gⁿ*ε = ε*g^–n  = ε*g^4–n

 

Группа симметрий правильного восьмиугольника

Пусть A₁,…, A₈ – вершины правильного восьмиугольника, l₁,…, l^'₄ – его оси симметрии.

Рис I.2.

Рассмотрим группу симметрий правильного восьмиугольника. Она состоит из 16 элементов: 8 поворотов вокруг центра на углы, кратные π/4, и 8 отражений вокруг осей l₁, l^'₁, l^'₂,…, l₄, l^'₄. Обозначим ее O₁₆. Набор вершин {A₁, A₂,…, A₈,} будем обозначать A₍₈₎.

Пусть h – поворот квадрата на π/4 по часовой стрелке; ε – отражение квадрата около оси l^'₄. Очевидно, h и ε – образующие группы O₁₆; O₁₆ = {h^k, h^k*ε}, где k = 1,…,8.

Лемма I.3. h⁸ = e;  h*ε*h = ε; h^k*ε = ε*h^8–k

Отметим, что h² = поворот на π/2 – образующая группы симметрий квадрата C₈. Подгруппа {(h)^2k, (h)^2k*ε} изоморфна группе C₈. Группу O₁₆ можно рассматривать как расширение группы симметрий квадрата C₈ с помощью элемента h (поворота на π/4).

 

Группа симметрий двойной квадратной пирамиды

Рис I.3.

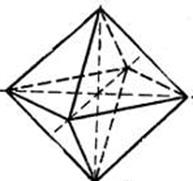
Двойная квадратная пирамида состоит из объединения пирамиды с квадратным основанием и зеркально отражённой к ней. Обозначим её группу симметрий P₁₆. Она получается, очевидно, из группы симметрии квадрата C₈, не меняющей вершины, и зеркального отражения i относительно плоскости (переводящего верхний конец пирамиды в нижний и  обратно). Т.о P₁₆ = {g₁, g₂,…, g_8, ig₁, ig₂,…, ig₈}, где {g₁, g₂,…, g₈} = C₈.

Хотя O₁₆ и P₁₆ являются расширениями C₈, с помощью одного элемента, но они не изоморфны друг другу, т.к. для O₁₆ этот элемент имеет степень 8, а для P₁₆ – степень 2.

Изоморфное представление группы симметрий квадрата

Обозначим набор чисел {3ⁿ (mod 10); n=1, 2, 3, 4} (={3, 9, 7, 1}) как N₍₄₎. (Здесь и далее все числа берутся по mod 10; если не оговорено обратное).

Рассмотрим следующие преобразования набора {3ⁿ} в себя:

g_(k,+)(3ⁿ) = 3^{n+k (mod 4)}; k= 1, 2, 3, 4 (умножение на 3^k)

g_(k,–)(3ⁿ) = 3^{–n+k (mod 4)}; k= 1,.. ,4 ("отражение" и умножение на 3^k)

Этих преобразований 8; они образуют группу. Обозначим ее NC ₈.

Лемма I.4. Действие преобразований g_(k,+) , g_(k,–) на N₍₄₎ (= {3ⁿ}) таково:

g_(k,+) (3ⁿ ) = 3^n+k  = 3^k*3ⁿ

g_{(k, –)} (3ⁿ ) = p(2^k*3ⁿ), где p(x) – число, сопоставляемое x по правилу p: 2ⁿ → 3ⁿ (это даёт 8 → 7, 2 → 3, 4 → 9, 6 → 1)

Т.о. действие g_(k,+) – это (обычное) умножение на 3^k; действие g_(k,–) – это умножение на 2^k и ещё некоторое обращение результата по правилу 2ⁿ → 3ⁿ.

Лемма I.5. Обозначим g_(1,+)  как g^~; тогда g_(k,+)  =(g^~)^k. Обозначим g_{(0, –)} как ε^~; тогда g_(k,–) = (g^~)^k *ε^~.

Теорема I.1. NC₈ изоморфна C₈.

Доказательство. Изоморфизм устанавливается отображением 

g^k  ↔ (g^~)^k; g^k*ε ↔ (g^~)^k*ε^~

Итак, группу NC₈ симметрий набора чисел {3ⁿ} можно рассматривать как изоморфное представление группы C₈ симметрий квадрата. При этом преобразования g_(k,–) соответствуют в группе C₈ отражениям около оси l_k+1.

Теорема I.1'. Поставим числа {3, 9, 7, 1} (= 3¹, 3², 3³, 3⁰) в вершины квадрата A₁, A₂, A₃, A₄. так, как указано на рис. I.4. Тогда действие на квадрате преобразования gÎC₈ (поворот на π/2) соответствует умножению на 3 в наборе {3ⁿ}, т.е. действию g^~ÎNC₈. Действие g^k*ε на квадрате (т.е. отражение относительно оси l_k+1) соответствует действию g_{(k, –)} на числах. Т.о. пара {NC₈, N₍₄₎} изоморфна паре {C₈, A₍₄₎}, где A₍₄₎= {A₁, A₂, A₃, A₄} – вершины квадрата.

Рис. I.4.

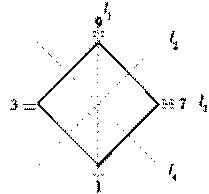
Изоморфизм C₈ ↔ NC₈ определяет действие группы симметрий квадрата C₈ на наборе чисел {3ⁿ}. Повороты из группы C₈ реализуются как (обычные) умножения чисел на 3ⁿ, а отражения из группы C₈ реализуются как умножения на числа 2^k и обращение результата по правилу 2ⁿ → 3ⁿ (что является для чисел некоторым аналогом геометрического отражения).

И обратно, можно считать, что группа NC₈ преобразований чисел {3ⁿ} действует на квадрате A₍₄₎. При этом, очевидно, преобразования g_(k,+) это повороты на k*(π/2); преобразования g_(k,–) – отражения.

 

Числовой октаэдр и его группа симметрий

 

Набор первых десяти чисел {1, 2, 3,… 10} естественным образом разбивается на две части: пару {5, 10} и восьмёрку {3ⁿ, 2ⁿ}. Будем обозначать набор {3ⁿ, 2ⁿ} как N₍₈₎ и называть его числовым октаэдром.

Несколько лемм, касающихся степеней чисел 3 и 2.

Лемма II.1. 1). 3^m+4 = 3^m (mod 10); 2^m+4 = 2^m (mod 10)

2). 3^k * 2ⁿ = 2 ^{–k+ n (mod 4)}  (mod 10)

Лемма II.2. 1). 6*n = 1*n (mod 5) = n или n +5 (mod 10). Таким образом, умножение на 6 оставляет чётные числа на месте, по mod 10, а нечётные переводит в "дополнение"; является некоторым аналогом геометрического отражения.

2). Если y=3x, то x=2y (mod 5). Таким образом, умножение на 2 является некоторым аналогом деления на 3.

Здесь и далее, если особо не оговаривается, числа берутся по mod 10, а показатели степеней чисел 3 и 2, учитывая лемму II.1.1, по mod 4.

¤-умножение чисел {3ⁿ, 2ⁿ}

Введём в числовом октаэдре- наборе чисел {3ⁿ, 2ⁿ} (={3, 9, 7, 1, 2, 4, 8, 6}) некоторое умножение, превращающее его в группу. А именно, отобразим взаимно-однозначно группу симметрий квадрата C₈ на N₍₈₎ (т.е. представим элементы C₈ степенями троек (повороты) и двоек (отражения)), следующим образом:

e      g     g²     g³            ε      g*ε    g²*ε    g³*ε

3⁴    3¹    3²     3³             2⁴      2¹      2²       2³

1     3     9      7              6       2       4       8

Обозначим это соответствие λ. λ(g^k) =3^k; λ(g^k*ε) =2^k; т.о. поворотам g^k из группы C₈ поставлены в соответствие в N₍₈₎ степени 3^k; отражениям g^k*ε – степени 2^k. λ(e) =1; λ(ε) = 6.

Используя это отображение, в N₍₈₎ (={3, 9, 7, 1, 2, 4, 8, 6}) можно перенести групповую структуру из группы симметрий квадрата C₈; т.е. определить в N₍₈₎ умножение элементов, по которому набор чисел N₍₈₎ станет группой. Будем обозначать эту группу (т.е. набор чисел N₍₈₎ с внесённой в него операцией умножения) как N₈.

Обозначим это умножение через ¤ и выпишем в явном виде:

3^k ¤ 3^l   (→ g^k*g^l)                                = 3^k+l = 3^k*3^l

3^k ¤ 2^l   (→ g^k*g^l*ε = g^k+l*ε)                = 2^k+l

2^k ¤ 3^l   (→g^k*ε*g^l = g^k*g^4–l*ε = g^k-l*ε) = 2^k–l = 2^k*3^l

2^k ¤ 2^l   (→g^k*ε*g*ε^l = g^k*g^4–l)             = 3^k–l

Сопоставим ¤ с обычным умножением чисел.

Лемма II.3.

1) ¤-умножение справа на 3^l действует как обычное умножение на 3^l (см. 1 и 3 строки).

2) ¤-умножение справа на 2^l таково:

3^k ¤ 2^l        = 3^k*2^l          для k = 2, 4;

               = 10 – 3^k*2^l  для k = 1, 3;

2^k ¤ 2^l        = 15 – 2^k*2^l    для k = 1, 3;

               =  5 + 2^k*2^l     для k = 2, 4;

Итак, x¤y = или x*y (обычное умножение), или (10 – x*y), или (5 + x*y), или (15 – x*y).

Обращение элементов N₈ по ¤-умножению таково: (3^k)^–1 = 3^–k; (2^k)^–1 = 2^k.

¤-умножение некоммутативно.

{3ⁿ} является подгруппой N₈ по ¤-умножению, изоморфной подгруппе поворотов в C₈.

Группы симметрий числового октаэдра (набора {3ⁿ, 2ⁿ})

Поскольку N₈ является группой (по ¤-умножению), то на ней может быть определено действие двух групп (R и L) сдвигов слева и справа, а именно:

R_g : x → x*g^–1; 

L_g : x → g*x

Отображения g→R_g и g→L_g являются изоморфизмами групп; т.о. представлениями действия группы N₈ на {3ⁿ, 2ⁿ} = N₍₈₎.

Выпишем действие R на числовом октаэдре N₍₈₎ в явном виде:

3^k_пр: 3ⁿ → 3^n–k; 2ⁿ → 2^n+k;

2^k_пр: 3ⁿ → 2^n+k; 2ⁿ → 3^n–k

Нетрудно видеть, что 3^k_пр действует на элементы {3ⁿ, 2ⁿ} как (обычное) умножение на 3^–k; 2^k_пр являются отражениями: (2^k_пр)² = ε.

Аналогично действие L на N₍₈₎:

3^k_лв: 3ⁿ → 3^n+k;   2ⁿ → 2^n+k;

2^k_лв: 3ⁿ → 2^{–n +k}; 2ⁿ → 3^–n+k

L и R (как и N₈) изоморфны группе симметрий квадрата C₈, и т.о. каждая из них определяют представление C₈ в виде преобразований- симметрий числового октаэдра N₍₈₎.

± представление группы N₈ (C₈)

Сопоставим числам 3^k пары (k, +); числам 2^l  пары (l, –), т.е. полагая 2^l как бы отрицательными степенями тройки.

На наборы (k, t), где k = 1, 2, 3, 4; t = +, – можно перенести ¤-умножение из {3ⁿ, 2ⁿ} (будем обозначать его тоже ¤). Оно будет таким:

(k, +) ¤ (l, –) = (k+l, +); (k, +) ¤ (l, –) = (k+l, –)

(k, –) ¤ (l, +) = (k–l, –); (k, –) ¤ (l, –) = (k–l, +)

Т.о. на {(k, t)} задаётся структура группы, изоморфная N₈, а, значит, и C₈.

Группа симметрий квадрата и десятичная система счёта

Изоморфизм группы симметрий квадрата и группы некоторых симметрий набора чисел {3ⁿ, 2ⁿ} (умножение на 3^k, и "умножение с отражением" на 2^k) обусловлен тем, что для всякого числа g имеет место g⁵ = g (mod 10); т.о. степени тройки и двойки повторяются (по mod 10), с периодом 4; и такое же свойство имеют элементы группы квадрата: g⁵ = g.

Т.о. группа преобразований квадрата связана с десятичным представлением чисел.

"Китайские" симметрии

Определим для чисел {1, 2, 3,… 10} функции ls, ie, ht:

ls (x) = (10 – x); ie (x) = (15 – x); ht (x) = (5 + x)

(здесь, как и везде, все числа берутся по mod 10; если не оговорено обратное):

Нетрудно видеть, что все три функции ls, ie, ht отображают множество {1, 2, 3,… 10} в себя, притом взаимно-однозначно.

Лемма II.4. Набор {e, ls, ie, ht}, рассматриваемых как операторы на множестве {1, 2, 3,… 10}, где e – тождественное отображение, образует группу, все элементы которой имеют второй порядок (являются отражениями).

Нетрудно проверить, что набор этих операторов замкнут, ассоциативен и каждый из них имеет обратный, что является определением группы. Замкнутость следует из очевидных соотношений ls*ie = ht; ls*ht = ie; ht*ie = ls; существование для каждого оператора обратного (совпадающего с ним самим) следует из соотношений ls² = ie² = ht² = e.

Обозначим эту группу H_кит; она коммутативна, изоморфна подгруппе симметрий правильного тетраэдра относительно его трёх осей. H_ls = {e, ls} является её подгруппой.

Действие H_кит на наборе {3ⁿ, 2ⁿ} (т.е. на числовом октаэдре N₍₈₎) не выводит за него. Числа 5 и 10 являются неподвижными точками преобразований ls, ie, ht. Далее будем рассматривать H_кит (={e, ls, ie, ht}) на числовом октаэдре; она является там подгруппой L.

Выпишем действие ls, ie, ht на числовом октаэдре N₍₈₎ в явном виде:

ls: 3ⁿ → 3ⁿ⁺²; 2ⁿ → 2ⁿ⁺² (оператор 3²_лв = 3²_пр)

ie: 3ⁿ → 2^–n+2; 2ⁿ → 3^–n+2 (оператор 2²_лв)

ht: 3ⁿ → 2^–n; 2ⁿ → 3^–n (оператор 2⁰_лв)

По функциям ls, ie, ht можно задать соответствующие отношения пар чисел, именно ls^*(x, y), если y = ls (x); для ie и ht аналогично. Будем называть эти отношения (пары чисел) ло-шу, инь-ян и хэ-ту соответственно. Т.о. ло-шу пары это (1, 9), (2, 8),…; инь-ян пары это (1, 4), (6, 9),…; хэ-ту пары это (1, 6), (2, 7),… Названия введены по соответствующим фигурам, известным в китайской нумерологии.

Взаимную связь отношений ло-шу, инь-ян, хэ-ту иллюстрирует лемма:

Лемма II.4'. 1). Пусть {X, Y, Z} – три числа из набора {1,…,10}. Пусть в треугольнике XYZ две стороны представляют какие-либо два из отношений хэ-ту, ло-шу, инь-ян. Тогда третья сторона представляет оставшееся отношение.

1'). Пусть g₃ = g₁*g₂. Пусть g₁, g₂ – какие-либо две из симметрий хэ-ту, ло-шу, инь-ян. Тогда g₃ представляет собой третью симметрию.

Лемма следует из соотношений ls*ie = ht; ls*ht = ie; ht*ie = ls.

Отношения инь-ян, ло-шу, хэ-ту связаны с соотношениями между степенями чисел 3 и 2. Это демонстрируют следующие леммы:

Лемма II.5. 1). Умножение каждого числа пары (x, y) на 3 сохраняет отношение ло-шу, инь-ян, хэ-ту.

2). {3^m, 3ⁿ}, {2^m, 2ⁿ}находятся в отношении ло-шу ↔ |m – n| =2.

2'). {3^m, 2ⁿ}находятся в отношении инь-ян или хэ-ту ↔ (m – n) делится на 2.

Лемма II.6.

1). Пусть ls^*(x, y). Тогда ht^*(2x, 3y) для x нечётного, 2x = 3y (mod 10) для чётного.

2). Пусть ie^*(x, y). Тогда ht^*(2x, 3y) для x чётного,  2x = 3y (mod 10) для x нечётного.

3). Пусть ht^*(x, y). Тогда ls^*(2x, 3y) для x нечётного; ie^*(2x, 3y) для x чётного.

Введенное выше ¤-умножение в {3ⁿ, 2ⁿ} оказывается связанным с "китайскими" симметриями, а именно, x¤y равняется либо простому произведению x*y, либо функциям ls, или ie, или ht от него (см. лемма II.3.2).

Поскольку ¤-умножение чисел {3ⁿ, 2ⁿ} изоморфно умножению в группе симметрий квадрата (по построению), то и группа C₈ также оказывается связанной с "китайскими" симметриями ls, ie, ht, именно: через них могут быть выражены (в обратном представлении) произведения элементов группы C₈ на отражения справа (см. ту же лемму).

Ещё несколько соотношений между ¤-умножением и симметриями ls, ie, ht:

Лемма II.7. Пусть x ¤ y = z. Тогда

1). p(x) ¤ y = p(z), если p – ls, или ie, или ht.

Т.о. p(x ¤ y) = p(x) ¤ y; операторы ls, ie, ht, действующие слева, можно выносить за скобки при  ¤-умножении.

2). x ¤ ls(y) = ls(z).

2'). x ¤ ht(y) = p₂(z), где p₂ – ht или ie

      x ¤ ie(y) = p₂(z), где p₂ – ht или ie

3). p₁ (x) ¤ p₂(y) = z или p(z); p₁, p₂ -– ht или ie; p – ls. (Т.е. изменение в ¤- произведении обеих сомножителей на их ht или ie дополнения либо оставляет результат без изменения, либо меняет его по ls).

3'). p₁ (x) ¤ p₂(y) = z или p(z); p₁ – ht или ie, p₂ – ls, ie, ht; p – ht или ie.

Основная группа симметрий числового октаэдра

Расширим группу симметрий L числового октаэдра, добавив к ней оператор 2⁰_пр, а затем все его произведения на элементы группы L. Обозначим получившуюся группу из 16 элементов как N₁₆ и назовём основной группой симметрий числового октаэдра. Очевидно, что L (т.о. и H_кит) является подгруппами N₁₆.

Геометрически N₁₆ можно представлять как объединение группы симметрий квадрата с некоторым отражением; например, как группу симметрий двойной квадратной пирамиды (см. выше). Добавленная симметрия реализуется как отражение  этой фигуры относительно квадрата. Т.о. N₁₆ изоморфна P₁₆.

Фундаментальные тетраэдры

Будем называть фундаментальными тетраэдрами четвёрки чисел {1, 4, 9, 6} (ФТ₁) и {3, 2, 7, 8} (ФТ₂); а также их расположения в вершинах правильных тетраэдров (рис. II.2)

Рис. II.2. ФТ₁                                               ФТ₂.

  

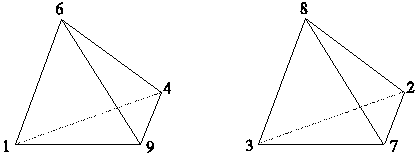
Очевидно, что. ФТ₁ = {3²ⁿ ; 2²ⁿ}; ФТ₂ = {3²ⁿ⁺¹; 2²ⁿ⁺¹}

Теорема II.1.

1) Пусть {x₁, x₂, x₃, x₄} = ФТ. Тогда для всякого числа x из ФТ, пары (x, y), (x, z), (x, u), где  y,  z,  u – оставшиеся числа из этого ФТ, представляют собой пары инь-ян, ло-шу, хэ-ту.

Пример: (1, 4), (1, 9), (1, 6).

1') (следствие) ФТ_i инвариантны относительно группы H_кит (= {e, ls, ie, ht}).

2). Действие элементов группы H_кит на ФТ_i представляют собой отражения ФТ_i относительно его осей симметрии l₁, l₂, l₃.

При этом отражение относительно оси l₁ представляет собой инь-ян симметрию, относительно l₂ – ло-шу симметрию, относительно l₃ – хэ-ту симметрию.

Рис. II.3. Отражения относительно осей симметрии тетраэдра

                     ФТ₁                                             ФТ₂

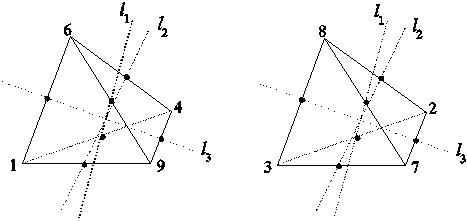
Теорема II.2.

1) ФТ₂ = 3*ФТ₁, ФТ₁ = 3*ФТ₂

ФТ₂ = 7*ФТ₁, ФТ₁ = 7*ФТ₂

ФТ₁ = 9*ФТ₁, ФТ₂= 9*ФТ₂

ФТ₁ = 1*ФТ₁;  ФТ₂= 1*ФТ₂

1') (следствие) ФТ_i при действии операторов 3ⁿ_пр, либо инварианты (для n = 2k), либо  переходят друг в друга (для (для n = 2k+1)). Поскольку операторы 3ⁿ_пр (¤-умножение справа на 3ⁿ) действует как обычное умножение на 3ⁿ.

Эти свойства показывают, что ФТ_i являются естественными объектами (в числовом октаэдре), обладающими некоторыми свойствами симметрии.

Орбиты и инвариантные объекты в числовом октаэдре

Орбитами группы G, действующей на множестве X, называются множества {g_ix}, где x Î X фиксировано, а g_i пробегают всю G. X распадается на объединение непересекающихся орбит. Орбиты, очевидно, инвариантны при действии на них G.

Примеры:

1) Подмножества нечётных чисел N₍₄₎ (= {3ⁿ}) и чётных чисел N₍₄₎^* (= {2ⁿ}) являются орбитами в N₍₈₎ для групп 3^k_пр и 3^k_лв (правых и левых сдвигов на 3^k).

2) ФТ₁ и ФТ₂ являются орбитами в N₍₈₎ при действии в ней группы H_кит.

Теорема II.3. Если множество X, на котором действует G, распадается относительно подгруппы H на (непересекающиеся) орбиты, X = UX_n, то действия сопряжённых к H классов эти орбиты либо оставляют их на месте, либо переводят друг в друга.

Например, подмножества нечётных N₍₄₎ и чётных чисел в N₍₈₎, являющиеся орбитами в числовом октаэдре N₍₈₎ для подгруппы 3^k_пр (3^k_лв), переходят друг в друга при действии на них элементов из 2^k_пр (2^k_л) – классов, сопряжённых к подгруппам 3^k_пр (3^k_л) (т.е. при ¤-умножении их, справа или слева, на степени двойки).

 

Триграммное представление числового октаэдра

 

Триграммы и их числовые представления

Триграммами  называются фигуры

состоящие из трёх сплошных (ян) или прерывистых (инь) линий. Всех возможных триграмм 8; будем обозначать их набор TG₍₈₎.

Триграмма называется нечётной/ мужской, если в ней нечётное число сплошных (ян) линий (на рисунке это первые 4 ТГ); в противном случае она называется чётной/ женской.

Можно задавать числовое представление триграмм, сопоставляя им (восемь) чисел.

Со времен Г. Лейбница, одним из первых в Европе изучавших три- и гексаграммы, стало популярным представлять ТГ как двоичные записи чисел {0,…,7=2³ - 1}, полагая, что черта инь (–   –) соответствует 0, а ян (–––) 1 (или наоборот). Такое представление триграмм сохраняет их "двоичный смысл" и может применяться для их интерпретации в терминах двоичной логики. Вместе с тем, нетрудно видеть, что такое представление не сохраняет симметрий, действующих на фигурах ТГ – точнее, геометрические симметрии триграмм не переходят в "содержательные" симметрии чисел.

С другой стороны, при некотором представлении триграмм числами из набора {3ⁿ, 2ⁿ} - числового октаэдра оказывается, что симметрии триграмм переходят в рассмотренные выше симметрии числового октаэдра. (Дополнительные аргументы в пользу такого представления см. далее в Приложении).

Зададим следующее взаимно-однозначное отображение S триграмм на числа из набора {3ⁿ, 2ⁿ}:

Будем называть это отображение S-представлением.

В S-представлении "мужским" триграммам соответствуют нечётные числа (степени троек), "женским" – чётные (степени двоек). Подъём черты ян в мужской триграмме снизу вверх соответствует умножению на 3; подъём черты инь в женской триграмме снизу вверх соответствует умножению на 2. 

Симметрии в наборе триграмм

На наборе триграмм TG₍₈₎ действуют определённые преобразования, переводящие его в себя. Преобразование f (фань): триграмма "переворачивается" – отражается от центральной линии. Преобразование d (дуй): каждая черта ТГ переходит в противоположную, инь в ян и обратно. Преобразование s₁: нижняя черта ТГ переходит в противоположную; аналогично s₂, s₃. Очевидно, d = s₁*s₂*s₃. Далее, преобразование s₁₂ – 1 и 2 черты (счёт снизу) переходят в противоположные; аналогично s₂₃, s₁₃. Далее, f₁ = f*s₁ (1 черта переходит в противоположную и вся триграммы переворачивается); аналогично f₂, f₃. Далее, f₁₂ = f*s₁₂ (1 и 2 черты переходят в противоположные и вся триграмма переворачивается); аналогично f₂₃, f₁₃. Преобразование ε = f*d (изменение всех черт и переворачивание). Наконец, e – тождественное.

Примеры:

              f                              d = s₁*s₂*s₃                    f*s₁*s₂*s₃

Полученное множество преобразований замкнуто, имеет единичный элемент и для каждого элемента имеет обратный; т.о. образует группу. В ней 16 элементов; она неабелева. Обозначим её H₁₆.

Числовое представление группы H₁₆

Если отобразить триграммы на набор чисел {3ⁿ, 2ⁿ} по S-представлению, то группа симметрий триграмм H₁₆ отобразится в некоторую группу H₁₆^~ преобразований- симметрий числового октаэдра {3ⁿ, 2ⁿ}. Вот некоторые:

1) Симметрия ε = f*d (изменение всех черт и переворачивание) для ТГ переходит в симметрию ie (инь-ян) для чисел.

2) Симметрия s₁₃ (изменение 1 и 3 черты) для триграмм переходит в симметрию ls (ло-шу) для чисел.

3) Симметрия f*s₂ (изменение 2 черты и переворачивание) для триграмм переходит в симметрию ht (хэ-ту) для чисел.

4) Симметрия f*s₁₂ (изменение 1 и 2 черты и переворачивание) для триграмм переходит в оператор 3¹_лв, т.е *3 для нечётных чисел и *2 для чётных чисел.

5) Симметрия f*s₃ для триграмм переходит в оператор 3¹_лв*2⁰_пр для чисел, который действует как "перевод числа в ближайшее" для пар (1, 2), (3, 4), затем "переход через центр" и далее (7, 6), (9, 8). Симметрия f*s₁ действует аналогично в обратном направлении.

Итак, при числовом представлении триграмм по правилу S, ряд симметрий триграмм переходит в симметрии числового октаэдра.

Теорема III.0. Группа H₁₆^~  - это группа левых сдвигов, расширенная с помощью оператора 2⁰_пр, т.е. рассматривавшаяся выше основная группа симметрий числового октаэдра N₁₆.

Ввиду того, что группа N₁₆ может быть представлена как группа симметрий двойной четырёхугольной пирамиды, то так можно рассматривать и группу преобразований триграмм H₁₆.

Итак, набор триграмм TG₍₈₎ можно взаимно-однозначно отобразить, по правилу S, на числовой октаэдр N ₍₈₎, при этом группа симметрий триграмм H₁₆ отобразится на группу симметрий N₁₆. Т.о. пары (TG₍₈₎, H₁₆) и (N ₍₈₎, N₁₆) изоморфны.

Подгруппы H₁₆

Будем обозначать g = f*s₁*s₂, ε = f*s₁*s₃, d = s₁*s₂*s₃, i^e = f*s₁*s₂*s₃, l^s = s₁*s₃, h^t = f*s₂ (в числовой форме i^e, l^s, h^t соответствуют операторам ie, ls, ht; а g – оператору 3¹_лв; отметим l^s = g²).

Нетрудно заметить существование в H₁₆ ряда подгрупп.

Прежде всего, это группа H_лв, соответствующая в числовом представлении группе L операторов левого сдвига.

H_лв = {e, f*s₁*s₂*s₃, s₁*s₃, f*s₂, f*s₁*s₂, f*s₂*s₃, s₁, s₃}

= {e, g, g², g³, i^e, g*i^e, g²*i^e, g³*i^e}

Как и L, H_лв изоморфна группе симметрии квадрата C₈.

H_кит = {e, i^e, l^s, h^t} ={e, f*s₁*s₂*s₃, s₁*s₃, f*s₂} = {e, i, g², i*g²}. Подгруппа в H_лв.

H_чётн = {e, s₁*s₂, s₁*s₃, s₂*s₃, f, f *s₁*s₂, f*s₁*s₃, f*s₂*s₃}. Подгруппа симметрий триграмм, сохраняющих их чётность.

Группа H_чётн чётных симметрий триграмм, как и H_лв, изоморфна группе симметрий квадрата C₈. Этот изоморфизм групп устанавливается следующим соответствием:

e ↔  e;  g↔ f*s₁*s₂; g² ↔ s₁*s₃; g³ ↔ f*s₂*s₃ ;

ε ↔ f*s₁*s₃; g*ε ↔ s₁*s₂; g²*ε ↔ f ; g³*ε ↔ s₂*s₃

H_вращ = {e, f *s₁*s₂, s₁*s₃, f*s₂*s₃ }. Циклическая группа 4 порядка, изоморфная группе вращений квадрата {e, g, g², g³}. Она является подгруппой в H_лв и H_чётн одновременно

H_комм = {e, s₁*s₂*s₃, s₁*s₃, s₂} = {e, d, l^s, d* l^s, s₂} {e, d, g², d*g²}. H_комм представляет собой коммутатор группы H₁₆. Изоморфна группе отражений тетраэдра относительно его осей.

H_пр = {e, s₁, s₂, s₃, s₁*s₂, s₁*s₃, s₂*s₃, s₁*s₂*s₃}. Коммутативная группа из 8 элементов, имеющих порядок 2 (отражения), изоморфная прямому произведению групп Z₂ * Z₂ * Z₂.

H_ФТ = {e, f*s₁*s₂*s₃, s₁*s₃, f*s₂, s₂, s₁*s₂*s₃, f, f*s₁*s₃}

= {e, i^e, l^s, h^t, d, d*i^e, d*l^s, d* h^t}

=  {e, s₁*s₂*s₃, s₁*s₃, s₂, i^e, i^e*s₁*s₂*s₃, i^e*s₁*s₃, i^e*s₂}

= замыкание H_кит при помощи f или при помощи d (=  s₁*s₂*s₃);

=  замыкание H_комм. (={e, s₁*s₂*s₃, s₁*s₃, s₂} при помощи i^e.

H_ФТ является группой инвариантности для фундаментальных тетраэдров ФТ₁ и ФТ₂ (рассматриваемых в триграммной форме); т.е. каждый элемент H_ФТ оставляет ФТ_i на месте; см. далее теорема V.1.

Все подгруппы H₁₆ можно рассматривать как подгруппы N₁₆, которой H₁₆ изоморфна (или, т.о. подгруппы группы симметрий двойной квадратной пирамиды).

Действие группы H₁₆ на фундаментальных тетраэдрах

Представим ФТ_i триграммами, заменив каждое число триграммой по правилу S.

Рис. III.1.

               ФТ₁                                           ФТ₂

 

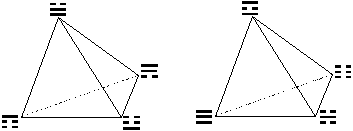
Теорема III.1. Все элементы группы H_ФТ = {e, f*s₁*s₂*s₃, s₁*s₃, f*s₂, s₂, s₁*s₂*s₃, f, f*s₁*s₃} переводят ФТ_i в себя. Т.е. тетраэдры ФТ₁ и ФТ₂ являются орбитами в TG₍₈₎ для группы H_ФТ.

Примечание. Группу, оставляющую на месте ФТ_i можно получить из замечания, что ФТ₂ переводится в себя симметрией f и группой H_кит (см. теорема II.1 выше или Рис. III.2 ниже), т.о. и их замыканием, которое и является группой H_ФТ. Поскольку H_ФТ переводит в себя ФТ₂, то, значит и ФТ₁.

Теорема III.1'. Элементы сопряжённого класса к H_ФТ переводят ФТ₁ ↔ ФТ₂.

H_ФТ^*= {s₁, s₃, s₁*s₂, s₁*s₃, s₂*s₃,  f*s₁*s₂, f*s₂*s₃, f*s₁, f*s₃}

Теорема III.2.

1) Действия элементов группы H_кит на ФТ_i являются отражениями ФТ_i относительно их осей симметрии l₁, l₂, l₃. (рис. III.2.). Действие i^e (инь-ян) это отражение относительно оси l₁; действие l^s (ло-шу) – относительно оси l₂; действие h^t (хэ-ту) – относительно оси l^s.

Рис. III.2.

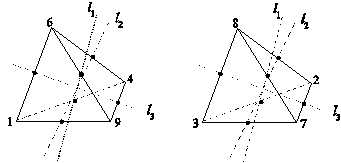
2) Представления Т_i: H_ФТ → H_тетр (группа симметрий тетраэдра) являются гомоморфизмами; с ядрами {e, f*s₁*s₃} и {e, f} для ФТ₁ и ФТ₂ соответственно.

Теорема III.3.

1). "gÎH_ФТ  g*i^e*g^-1 = i^e; где i^e = f*s₁*s₂*s₃ = инь-ян симметрия

1'). "gÎH_ФТ^*  g*i^e*g^-1 = h^t где h^t = f*s₂ = хэ-ту симметрия;

Таким образом, g*i*g^-1 либо оставляет инь-ян симметрию i^e на месте, либо переводит её в хэ-ту симметрию.

2). "gÎH_ФТ  g*h^t*g^-1 = h^t; где h^t = f*s₂ = хэ-ту симметрия

2'). "gÎH_ФТ^* g*h^t*g^-1 = i^e где i^e = f*s₁*s₂*s₃ = инь-ян симметрия;

Таким образом, g*h^t*g^-1 либо оставляет хэ-ту симметрию h^t на месте, либо переводит её в инь-ян симметрию.

3). "gÎH₁₆ g*l^s*g^-1 = l^s ; где l^s = s₁*s₃ = ло-шу симметрия. (Поскольку s₁*s₃ (ло-шу) коммутирует со всеми операторами из H₁₆).

Следствие. "g из подгруппы H_ФТ и всякого x из подгруппы H_кит имеет место g*x*g^-1 = x; т.е. действие g*x*g^-1 для элементов H_ФТ оставляет каждую из симметрий инь-ян, ло-шу, хэ-ту инвариантной.

 

Квазисимметрии расположений числового октаэдра

 

Квазисимметрии

Фигура на плоскости или в пространстве называется симметричной, если существуют движения (повороты или отражения), переводящие её в себя. Множество таких движений образует группу. Очевидно, что симметричные фигуры имеют одинаковые (совмещаемые движением) части; и их тем больше, чем выше степень симметрии фигуры (число элементов в её группе симметрии).

Вместе с тем, существуют фигуры, с виду обладающие некоторой симметрией- сходством частей, но никаким (обычным) движением на плоскости или в пространстве (кроме тождественного) в себя не переводимые.

Целый класс таких объектов можно получить, объединяя в одну (несимметричную) несколько фигур, по отдельности симметричных – например, круг и квадрат, правильный треугольник и т.д. Все фигуры такого типа характеризуются тем, что их части могут быть переведены в себя некоторыми движениями, но не существует движений, переводящих всю фигуру в себя.

Расширить класс "симметричных с виду" объектов, не обладающих симметрией в обычном смысле, можно, рассмотрев фигуры, составленные из частей с "нагруженными" дополнительными объектами, например, числами (рис. IV.1а), или цветами (рис. IV.1б).

           Рис. IV.1а.                                           Рис. IV.1б.

                                   

 

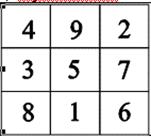
Будем называть фигуру A квазисимметричной, если её можно представить в виде объединения частей A_i, нагруженных свойствами p_i, A = U(A_i, p_i), так, что существуют движения (повороты или отражения) g_i^k частей A_i (возможно, всей фигуры) и преобразования q_i "нагрузок", для которых A_i переводятся себя, а свойства p_i преобразуются по q_i.

Для фигуры на рис IV.1 (квадрат с числами) таким преобразованием будет поворот на π/2 с одновременным умножением всех чисел на 3 (по mod 10). Для фигуры на рис IV.2 это будет поворот на π и одновременное изменение цветов частей на противоположные.

Преобразование фигуры A, состоящей из нескольких частей с нагрузками, A= U(A_i, p_i), будем называть квазигеометрическим, или квазисимметрией если оно состоит из движений или отражений её частей A_i, при одновременном изменении нагрузок p_i. Квазисимметрии являются обобщениями обычных движений фигур.

Квазисимметричные представления

Пусть на множество X действует группа его преобразований G. Тогда X распадается на непересекающиеся орбиты, X = UX_n, относительно действия группы G; X_n = {Gx_n}.

Поместим множество X на плоскость/ в пространство; или, что тоже, припишем его элементам координаты, "нагрузим" их числами (парами чисел для плоскости, тройками для пространства). В множестве ГX = {(x_k, p_k), x_kÎX, p_k - точки} естественным образом возникает представление G.

Поскольку X распадается на орбиты X_n, инвариантные относительно действия группы G, то таким будет и ГX, и его орбиты ГX_n также будут инварианты относительно G; другими словами, на этих орбитах будут действовать представления G; обозначим их ГG_n.

Орбиты ГX_n являются множествами точек на плоскости/ пространстве, таким образом, элементы ГG_n действуют как преобразования некоторых геометрических объектах в себя.

Представления группы G на погруженном в пространство множестве X называется квазисимметричным, если действия всех его g на орбитах ГX_n являются квазисимметриями (движениями или отражениями).

Отметим, что для выяснения квазисимметричности представления группы G (и характера этих квазисимметрий), достаточно изучить действие на ГX образующих G.

Разумеется, не для всякого расположения в пространстве элементов X, на котором действует группа G, соответствующее представление G будет квазисимметричным. Такие расположения можно строить, например, следующим образом. Пусть G – циклическая группа  порядка n с образующей g, действующая взаимно-однозначно на некотором X. Разместим элемент xÎX в точке p, а gx – в повёрнутой на угол 2π/n относительно некоторой точке O. Продолжая эту процедуру, мы разместим, очевидно, все точки X в вершинах правильного n-угольника, а все элементы gÎG –будут представлены поворотами на угол 2πk/n в плоскости вокруг точки O. Т.о. представление G будет геометрической симметрией.

Лишь немного сложнее будет случай, когда G является расширением циклической группы {g^k} n-го порядка с помощью некоторого отражения ε. Тогда аналогичные объекты в пространстве будут представлять собой уже два правильных n-угольника, преобразования которых по элементам группы g^k и εg^k будут поворотами на 2πk/n по отдельности – т.е. квазисимметриями. Поскольку при таком построении ε будет переводить один n-угольник в другой с помощью, очевидно, (геометрического) отражения, то и всё представление G на таком расположении X в пространстве будет квазисмметричным

Далее будут рассмотрены квазисимметрические представления некоторых групп на расположениях на плоскости числового октаэдра {3ⁿ, 2ⁿ}.

Квазисимметрии расположений в плоскости числового октаэдра при действии на нём группы симметрий квадрата

Как было показано выше, на числовом октаэдре N₍₈₎ может быть определено действие группы симметрий квадрата, именно, как действие ¤-умножения на степени 3 и 2 (слева или справа).

Для задания на каком-либо расположении числового октаэдра- набора чисел {3ⁿ, 2ⁿ} в плоскости действия группы C₈ достаточно определить действие её образующих – поворота на π/2 и отражения (в числовом представлении – операторов ¤-умножения на 3 и на 2).

Расположим набор чисел {3ⁿ, 2ⁿ} на плоскости в порядке ло-шу (рис. IV.2а). Определим на нём действие группы симметрий квадрата C₈ через её представление операторами ¤-умножения на степени 3 и 2 справа. Легко видеть, что ¤-умножение их справа на 3 (совпадающие с обычным умножением на 3), эквивалентно повороту на –π/2 (рис. IV.2а) а ¤-умножение их справа на 2 даёт: 3→4, 9→8, 7→6, 1→2; 2→1, 4→3, 8→9, 6→7 (лемма II.3); что эквивалентно отражению около оси l₃^' (рис. IV.4). ¤-умножение справа на 3^k совпадает с обычным умножением на 3^k; т.о. на ло-шу его реализуют повороты на –k*(π/2). ¤-умножение слева на 2^k реализуют отражения ло-шу вокруг осей l_4–k^' (k = 1, 2, 3, 4). Таким образом, это представление C₈ реализуется симметриями (движениями или отражениями) фигуры в целом.

Рис. IV.2. ¤-умножение чисел ло-шу справа на 3 (= обычные умножение)  = поворот на –π/2

→

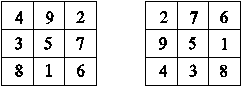
Другое представление действия C₈ на расположении N₍₈₎ можно получить через её представление операторами ¤-умножения на степени 3 и 2 слева.

¤-умножение слева на 3^k совпадает для нечётных чисел с обычным умножением на 3^k; т.о. на ло-шу оно реализуется поворотами на угол –k*(π/2); для чётных чисел оно реализуется как поворот ло-шу на угол k*(π/2). Т.о. ¤-умножение чисел ло-шу слева на 3^k реализуется поворотами круга для нечётных чисел и поворотами квадрата для чётных чисел; в разные стороны (рис. IV.3) – является квазисимметрией. ¤-умножение слева на 2^k реализуется на рассматриваемом расположении числового октаэдра, как и ранее, отражениями.

Рис. IV.3. ¤-умножение чисел ло-шу слева на 3^k реализуется поворотами нечётных и чётных чисел на угол k*(π/2) в разные стороны - квазисимметрией.

Можно изучать действие группы симметрий квадрата и на других расположениях числового октаэдра в плоскости. Некоторые из них рассмотрены далее в приложении "Симметрии расположений триграмм".

Квазисимметрии расположений в плоскости числового октаэдра при действии на нём группы симметрий правильного восьмиугольника

Расположим числа {3ⁿ, 2ⁿ} в вершинах восьмиугольника в порядке ло-шу (рис. IV.4).

Рис.IV.4.

Определим действие элементов O₁₆ на них.

Нетрудно видеть, что преобразование поворота на π/4 (т.е. представление образующей h) действует на наборе {3ⁿ, 2ⁿ} так: 3ⁿ → 2^–n–1, 2ⁿ → 3^–n. h^~(3ⁿ) = 2^–n–1; h^~(2ⁿ) = 3^–n.

Заметим, что h² = g = поворот на π/2 (образующая группы симметрий квадрата C₈). Поскольку поворот на π/2 на ло-шу можно представлять как умножение справа на 3^–1, то можно записать (h^~)² = 3^–1_пр; или h^~ = √3^–1_пр.

Нетрудно видеть, что ε (отражение около оси l^'₄) действует на {3ⁿ, 2ⁿ} так: 3ⁿ ↔ 2ⁿ; ему соответствует оператор 2⁰_пр.

Группа O₁₆ является расширением группы симметрий квадрата C₈ с помощью элемента h (поворота на π/4), и, соответственно, изоморфная ей группа O^~₁₆ (действующая на числовом октаэдре) тоже может рассматриваться как расширение основной группы симметрии числового октаэдра, с помощью оператора h^~, действующего на числовом октаэдре как 3ⁿ → 2^–n–1, 2ⁿ → 3^–n, = √3^–1_пр.

Квазисимметрии расположений числового октаэдра при действии на нём группы симметрий двойной пирамиды

Заменим, для наглядности, числовой октаэдр на 8 триграмм, тогда действующая на нём группа симметрий двойной пирамиды перейдёт в группу H₁₆ (см. выше).

Рассмотрим расположение 8 триграмм в плоскости в порядке ло-шу (рис.IV.4). Нетрудно видеть, что все симметрии из H₁₆ реализуются на этой фигуре либо как движения квадрата, либо как их комбинации, действующие по отдельности на квадратах, соответствующих чётным и нечётным числам – т.е., как квазисимметрии. Например, s₁*s₃ представляет собой поворот на π/2; f*s₁*s₃ – комбинация отражений вокруг осей l₁ и l₄.

Можно изучать квазисимметрии представлений группы квадрата/ двойной пирамиды и на других расположения числового октаэдра (или его изоморфного ТГ-представления, что иногда бывает нагляднее). Некоторые из них рассмотрены далее.

Квазисимметрии расположений числового октаэдра в спин-пространстве при действии на нём группы симметрий двойной пирамиды

Нагрузим точки обычного трёхмерного пространства значениями + и –; или будем располагать в каждой из них пары чисел, связанных некоторым ±- отношением. Будем называть полученный объект спин-пространством.

Нетрудно видеть (рис. IV.5), что группа симметрий двойной квадратной пирамиды P₁₆ изоморфна группе симметрий квадрата в спин-плоскости, а именно, отображение зеркальной симметрии i относительно плоскости квадрата (меняющее местами верхнюю и нижнюю вершины), перейдёт в изменение знаков у точек квадрата; подгруппа P₁₆, соответствующая группе симметрий квадрата, будет действовать обычным способом.

Рис. IV.5

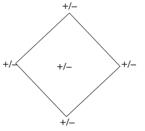
Разместим числовой октаэдр на спин-плоскости в вершинах квадрата следующим образом (рис. IV.6), добавив в центр квадрата пару 5/10.

Рис.IV.6.

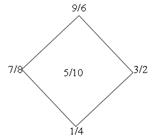
Легко видеть, что симметрии двойной пирамиды при представлении её симметриями числового октаэдра (т.е. группой N₁₆; см. выше) на таком объекте переходят или в обычные симметрии или в квазисимметрии. Так, ie симметрии соответствует зеркальное отражение i, действующее так: 5 ↔ 10, 1 ↔ 4, 3 ↔ 2, 9 ↔ 6, 7 ↔ 8; т.е. переставляющее верхние числа с нижними ("меняющее знак"); ¤-умножение слева на 3^k реализуются обычными поворотами на углы –k*(π/2) для (квадрата) нечётных чисел, и на углы k*(π/2) для (квадрата) чётных чисел; ¤-умножение слева на 2^k реализуется отражением квадрата. Комбинации ie с группой симметрий квадрата реализуются поворотами или отражениями квадрата с одновременным изменением чисел на дополнительные к ним ("знака точек").

Заменив числовой октаэдр N₍₈₎ на восемь триграмм TG₍₈₎, а группу N₁₆ на группу H₁₆, мы получим представление H₁₆ в виде квазисимметрий квадрата ТГ в спин-пространстве.

 

Симметрии в расположениях триграмм

 

В древнекитайской культуре имелся ряд составленных из чисел и фигур объектов: три- и гексаграммы, пентаграмма, квадрат ло-шу и т.д. В Европе XVIII века гексаграммы стимулировали популяризацию Лейбницем открытой незадолго до этого рядом математиков двоичной системы счисления[1].

 

Круговые порядки триграмм

В китайской культуре известны два расположения триграмм по кругу: т.н. порядки Фу Си (рис ПI.1а) и Вэнь вана (рис V.1б).

Рис. V.1.

      а) порядок Фу Си                      б) порядок Вэнь вана

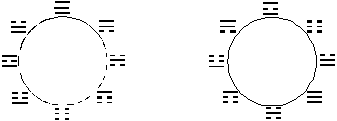
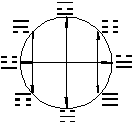
Порядок Фу Си обладает заметной симметрией[2], например, при отражении относительно центра круга триграммы преобразуются по правилу замены всех черт на противоположные. (Описание других симметрий в порядке Фу Си см. ниже). В отличие от него, порядок Вэнь вана не обладает столь явно выраженной (геометрической) симметрией. Вместе с тем, некоторые симметрии в расположении Вэнь вана всё же имеются. Например, линии на рис V.2 связывают пары триграмм, находящихся в отношении "переворачивания" (фань) и изменения черт на противоположные (дуй). То есть, симметрия фань*дуй (f*d) действует на круговой порядок Вэнь вана как (квази)симметрия, обозначенная на рисунке V.2 стрелками. (Описание других симметрий в порядке Вэнь вана см. ниже).

Рис. V.2. Действие f*d на расположении ТГ Вэнь вана

 

Числовое представление триграмм

Со времен Лейбница стало популярным представлять ТГ как двоичные записи чисел {0,…,7=2³ - 1}, полагая, что черта инь (–   –) соответствует 0, а ян (–––) 1 (или наоборот).

Такое представление сохраняет "двоичный смысл" триграмм и может применяться для их интерпретации в терминах двоичной логики. Вместе с тем, такое представление не сохраняет симметрий, действующих на фигурах ТГ – т.е. большинство геометрических симметрий не переходят в "содержательные" симметрии чисел. Кроме того, при таком представлении число 5 не играет выделенной центральной роли, как это имеет место в китайской нумерологии ("учении о символах и числах"; сян шу чжи сюэ). Наконец, при использовании такой "кодировки" порядок Вэнь вана переходит в кажущийся хаотичным набор чисел (см. рис. ПI.3б).

Можно попытаться найти числовое представление триграмм, которое более точно выражало бы "суть" триграмм, (проявляющуюся в т.ч. в их симметриях) и "числовую специфику" китайской культуры.

Для ранней китайской культуры характерно сопоставление "Небо" → 3, "Земля" → 2. "Совершенномудрые обозначили Небо тройкой, а Землю двойкой…". Примем это как начало числового представления триграмм: Тянь (Небо) → 3, Кунь (Земля) → 2. Как сопоставлять числа триграммам дальше? В китайской нумерологии триграммы делятся на мужские и женские, а именно, триграммы с нечётным ("мужским") количеством непрерывных чёрт считаются "мужскими", с чётным – "женскими". Также для триграмм имеют место "родственные" отношения: Тянь (Небо) – "отец", мужские триграммы Чжэнь (Гром), Кань (Вода), Гэнь (Гора) – соответственно, 1-й, 2-й и 3-й "сын"; Кунь (Земля) – "мать", женские триграммы Сюнь (Ветер), Ли (Огонь), Дуй (Водоём) – соответственно, 1-я, 2-я и 3-я "дочь". Примем, что при сопоставлении триграммам чисел порождение очередной "мужской" триграммы соответствует умножению очередного числа на 3, "женской" – аналогично на 2. Т.е. "1-й сын" → 3*3; "2-й сын" → 3*3*3;…; "1-я дочь" → 2*2;… (mod 10).

Небо      Гром   Вода     Гора       Земля   Ветер   Огонь   Водоем

Отец      1 сын   2 сын   3 сын      Мать    1 дочь   2 дочь    3 дочь

Для 8 ТГ таким образом будут исчерпаны все числа из промежутка 1-10, кроме 5 и 10; то есть, они будут представлены числами набора {3ⁿ, 2ⁿ} - числовым октаэдром.

Обоснованиями такого соответствия триграммы ↔ числа являются, с точки зрения китайской нумерологии:

• мужские ТГ соответствуют нечётным числам, женские ТГ – чётным;

• числа 5, 10 играют выделенную роль – уже не появляются среди сопоставляемых чисел; как это и естественно. (Их зато можно сопоставить Великому пределу);

• симметрии триграмм (группа H₁₆) переходят в симметрии числового октаэдра.

Основным обоснованием такого числового представления триграмм является обнаружение с его помощью ряда красивых математических соотношений; в частности:

• в расположении Вэнь вана появляется числовая симметрия (рис. ПI.4) - в отличие от несимметричного представления Лейбница (рис. ПI.3б);

• в расположении Фу Си выявляется числовая симметрия, эквивалентная симметрии квадрата ло-шу (см. ниже).

S-представление тоже можно считать "двоичным", только вместо 0 и 1, как чисел, обозначающих инь-ян/ ложь-истина, принимаются числа 2 и 3. S-представление можно рассматривать как отображение десяти первых чисел {1,…,10} в десять фигур: 8 триграмм + символ Великого Предела (Тай-цзи); по указанному выше правилу.

Примечание. S-представление триграммы ↔ числа совпадает для четырёх триграмм, стоящих в расположении Вэнь вана на основных позициях (юг – север – восток – запад) с приведённым в работе комментатора И Цзина Мэн Си (–I в.)[3].

 

Числовые симметрии круговых порядков триграмм в S-представлении.

Числовое S-представление кругового порядка ТГ Вэнь вана обладает рядом заметных симметрий. Прежде всего, в нём имеется симметрия инь-ян (рис. V.4а), соответствующая в ТГ-виде преобразованию ε = f*d. Далее, связи на рисунках V.4б и V.4в дают отношения чисел (n, n+1) и ло-шу.

Рис V.3. Числовой порядок Вэнь вана.

       а) S-представление                        б) числа "по Лейбницу"

 

Рис V.4. Симметрии числового S-представления порядка Вэнь ванна

а) связь инь-ян          б) последовательные числа   в) связь ло-шу

 

В числовом S-представление порядка Фу Си также обнаруживаются симметрии:

Рис. V.5. Симметрии числового представления порядка Фу Си

     а) связь инь-ян                 б) 3^m ↔ 2^m                 в) связь хэ-ту

 

Дуально-спиральная симметрия

Будем называть фигуру Ф дуально-спирально симметричной, если она представляется в виде объединения непересекающихся фигур Ф₊ и Ф_– , таких что:

1) Ф₊ и Ф_– переходят друг в друга при повороте на π/2 относительно некоторого центра; 2) Ф₊ и Ф_– могут быть "соотнесены" с + и – (на них "нагружены" характеристики, соотносимые с + и –; например, цвета); 3) внутри Ф₊ содержится часть, соотносимая с –; внутри Ф_– содержится симметричная ей часть, соотносимая с +.

Стандартным примером дуально-спиральной симметрии является "китайский" чертеж Великого предела (Тай цзи), состоящий из инь и ян частей (его авторство и время появления дискуссионно) (рис. V.6а). Можно строить и другие аналогичные фигуры (рис. V.6б).

Рис V.6а) Чертеж Великого предела; б) Дуально-спиральная симметрия.

                                     

 

Симметрии ло-шу.

Для удобства будем далее представлять числа фигуры ло-шу расположенными на окружности (рис V.7а). Первой и основной симметрией этого объекта является ло-шу симметрия: числа, симметричные относительно центра, дополняют друг друга до 10. Ей соответствует симметрия триграмм s₁*s₃; а в числовом S-представлении – следующая симметрия числового октаэдра: 3^k → 3^k+2; 2^l → 2^l+2 (= ls = оператор 3²_пр) (рис V.7б).

Рис. V.7а. ло-шу……  .7б. ло-шу симметрия

                  

Симметричными получаются и другие геометрические объекты, образуемые при действии на ло-шу группы H₁₆. Так, симметрия f*s₂, отвечающая связи хэ-ту, даёт на фигуре ло-шу связи, показанные на рис V.8а; действие симметрии f*s₁*s₂*s₃ (инь-ян) даёт на ло-шу фигуру ПIII.2б. Вообще каждая симметрия из H₁₆ даёт на ло-шу некоторую геометрическую (квази)симметрию.

Рис. V.8.

а) хэ-ту симметрия на ло-шу         б) инь-ян симметрия на ло-шу

 

Рисунки V.9 иллюстрируют дуально-спиральную симметрию ло-шу. Если из чисел ло-шу вычесть 5 то фигура разделится на две симметричные части, состоящие из + и – чисел, в каждой из которых есть "вкрапления" другой (рис. V.9а). Изображение ло-шу по mod 5 (рис. V.9б) тоже выявляет его дуально-спиральную симметрию.

Рис. V.9а)                                        б)

 

Изобразим действие на фигуре ло-шу ещё некоторых симметрий из H₁₆.

Рис. V.10а) f*s₁*s₂                            б) s₁*s₂*s₃

Ряд геометрических симметрий на ло-шу также описывается симметриями числового октаэдра, хотя уже и не входящими в группу симметрий триграмм H₁₆. Так, поворот ло-шу на π/4 (т.е. применение к ло-шу образующей группы симметрий правильного восьмиугольника) может быть выражен формулой h: 3ⁿ → 2^–n–1, 2ⁿ → 3^–n

Очевидно, что h² есть поворот на π/2. Нетрудно видеть, что h² (в числовой форме) представляет собой (обычное) умножение всех чисел ло-шу на 3 (оператор 3_пр).

Будем называть фигуру, образованную на ло-шу соединением последовательных чисел путём ло-шу (рис. V.11а). Существование закономерности в пути ло-шу на какой-либо фигуре является признаком её дуально-спиральной симметрии.

Рис. V.11а) путь ло-шу                          б)

 

Фундаментальные тетраэдры

Будем располагать в вершинах фундаментальных тетраэдров (ФТ) не только числа (рис. V.12)., но и соответствующие им триграммы (рис. V.13).

Рис. V.12. ФТ₁                                              ФТ₂.

     

 

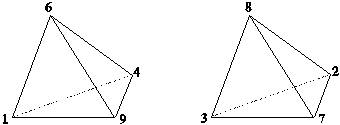
Рис. V.13. ФТ₁                                                 ФТ₂

     

 

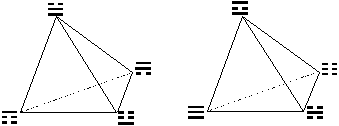
Можно заметить, что ФТ₂, состоящий из основных триграмм {Небо, Земля, Огонь, Вода}, является, в определённом смысле, "более важным" объектом чем ФТ₁.

Фигуры на ло-шу, образованные фундаментальными тетраэдрами симметричны (рис. V.14б). Фигуры на ло-шу, образованные последовательными числами ПЧ₁, ПЧ₂ тоже симметричны (рис. V.14а).

Рис. V.14

а) ПЧ на ло-шу                  б) ФТ на ло-шу

 

Симметрии кругового порядка триграмм Фу Си.

Расположение ТГ в круговом порядке ФуСи  обладает богатым набором симметрий, хорошо заметных и в триграммной (рис. V.15а), и в числовой (рис. V.15б) формах. В числовой форме выявляются симметрии (прежде всего дуально-спиральная), а также эквивалентность расположения Фу Си порядку ло-шу, которые в ТГ-форме практически не видны.

Рис. V.15а)         б) S-представление расположения ТГ Фу Си

 

Рис. V.16. Симметрии порядка Фу Си из группы H₁₆.

  а) инь-ян (f*s₁*s₂*s₃)                   б)   s₁*s₂*s₃      

  в) ло-шу (s₁*s₃)                            г) хэ-ту (f*s₂)

  д) умножение на 3 (f*s₁*s₂)                      е) s₂

 

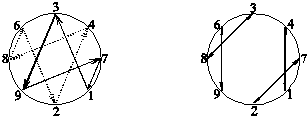
Рис. V.17. ФТ и ПЧ на Фу Си.

  а) фундаментальные тетраэдры     б) последовательные числа

 

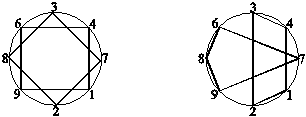
Покажем, что в расположении Фу Си есть дуально-спиральная симметрия. Cопоставив фигуру ло-шу и числовое S-представление Фу Си, замечаем, что их структуры похожи: во второй имеются такие же две симметричные части, как и в первой, только состоят они не из двух наборов последовательных чисел, с "вкраплениями" одного в другой, а из наборов чётных и нёчетных чисел, но с такими же "вкраплениями", на тех же местах (рис. V.18а и б). Более того, записав числа S-представления Фу Си в виде степеней тройки и двойки, обнаруживаем что их показатели образуют фигуру, подобную ло-шу, и имеющую характерный для объектов обладающих дуально-спиральной симметрией вид (рис. V.18в и г). Сопоставим, для большей наглядности, степеням тройки значения их показателей, а степеням двойки значения их показателей со знаком – (т.е. полагая степень двойки как бы отрицательной степени тройки). Тогда для порядка Фу Си, как и для фигуры ло-шу, имеются две последовательности + и – чисел, с вкраплением + внутри – и обратно (рис. V.18д).

Рис. V.18.. Дуально-спиральная симметрия Фу Си.

       а) ло-шу                             б)  Фу Си  

 

   в)  Фу Си      г) показатели степеней  д) показатели степеней

 

Дуально-спиральную симметрию порядка Фу Си выявляет и рассмотрение на нём (в S-представлении) пути ло-шу, обладающего здесь явной симметрией:

 2¹ → 2² → 2³ →2⁴   →   3⁴ → 3³ → 3² → 3¹

Можно указать простую формулу, связывающую (числовые) представления порядков Фу Си и ло-шу, т.е. указать способ преобразования одного порядка в другой. Эта формула такова:

3ⁿ → (10 – n);      2ⁿ → n.

Она напоминает логарифмирование.

Рис. V.19. Преобразование порядка Фу Си в ло-шу

                

               3ⁿ → (10 – n);      2ⁿ → n

Выявление в S-представлении порядка Фу Си дуально-спиральной симметрии и его изоморфизма с порядком ло-шу ещё раз показывают удобство S-представления для изучения триграмм.

 

Симметрии порядка Вэнь вана.

Расположение триграмм в круговом порядке Вэнь вана (рис. V.20) также обладает набором симметрий, заметных в триграммной и, особенно, в числовой форме. Как и для порядка Фу Си в числовом (S-) представлении порядке Вэнь вана выявляется ряд важных симметрий которые в триграммной форме практически не видны.

Рис. V.20. Расположение триграмм по Вэнь вану.

 

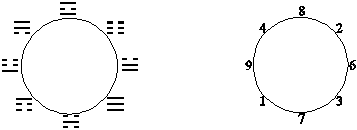
Рис. V.21. ПЧ и ФТ на диаграмме Вэнь вана.

 

Покажем, что в порядке Вэнь вана имеется дуально-спиральная симметрия. Заменим числа их остатками по mod 4 (рис. V.22а).

Рис. V.22.

                а)                                                         б)  

Путь ло-шу на рис. V.22а имеет симметричный вид:

      3^* → 2 → 1^* → 4     →    3 → 2^* → 1 →4^*

Выявление в числовом S-представлении кругового порядка Вэнь вана дуально-спиральной и других симметрий, практически незаметных в его триграммной форме, снова показывают удобство S-представления для изучения свойств триграмм. Кстати, предпринятое выше рассмотрение показывает, что кажущееся беспорядочным круговое расположение триграмм Вэнь вана обладает, на самом деле, богатым набором симметрий.

 

Связи порядков Фу Си и Вэнь вана

Фигуры связей инь-ян на расположениях Фу Си и Вэнь вана одинаковы (рис. V.23а). Хэ-ту фигура на Фу Си соответствует парам (n, n+1) на Вэнь ване (рис. ПVI.4б). Ло-шу фигура на Фу Си соответствует парам (n, n+2) на Вэнь ване (рис. ПVI.4в).

Рис. V.23.

а)  инь-ян на Фу Си           инь-ян на Вэнь ване 

  б)  хэ-ту на Фу Си                        (n, n+1) на Вэнь ване

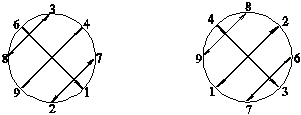
  в)  ло-шу на Фу Си                          (n, n+2) на Вэнь ване

 

Имеются и более тонкие дополнительные связи между этими двумя порядками чисел. А именно, фигуры, образованные фундаментальными тетраэдрами на Фу Си, совпадают с фигурами, образованными последовательными числами на Вэнь ване (рис. V.24г). И обратно, фигуры, образованные фундаментальными тетраэдрами на Вэнь ване совпадают с фигурами, образованными последовательными числами на Фу Си (рис. V.24д).

Рис. V.24. Связи порядка Фу Си и Вэнь вана (продолжение)

   г) ФТ на Фу Си                            ПЧ на Вэнь ване

 

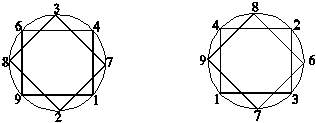
   д) ПЧ на Фу Си                          ФТ на Вэнь ване

 

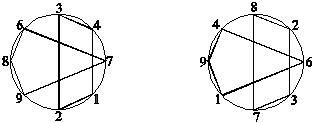
Нетрудно видеть, что:

1) ФТ₁ и ФТ₂ на Фу Си соответствуют на Вэнь ване ПЧ₁ и ПЧ₂.

2) ПЧ₁ и ПЧ₂ на Фу Си соответствуют на Вэнь ване ФТ₂ и ФТ₁.

Между прочим, 2) вовсе не является следствием 1) (!), и это еще раз показывает, что расположения чисел по Вэнь вану и Фу Си обладают глубокими внутренними связями.